Answered step by step
Verified Expert Solution
Question
1 Approved Answer
If A and B are both second-order tensors and t, u, v, and w are all vectors, prove the following identities using the indicial
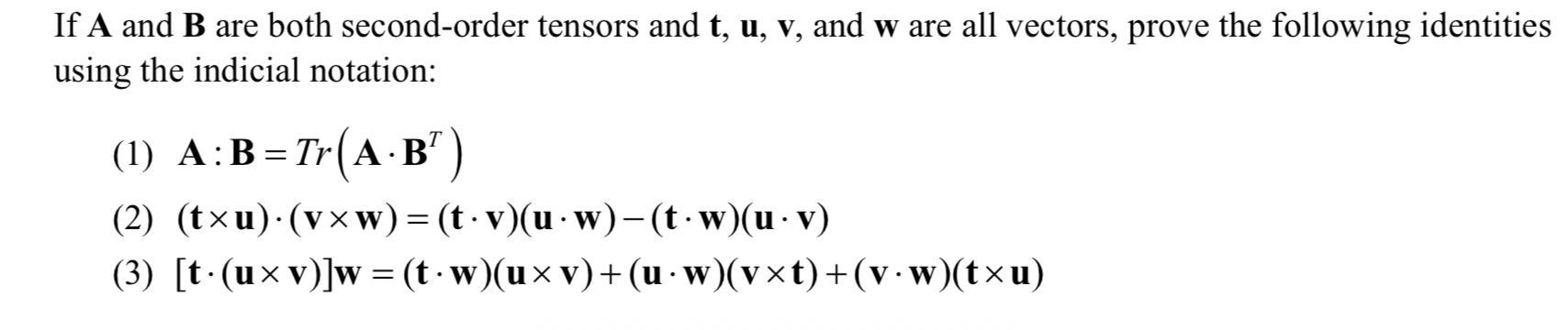
If A and B are both second-order tensors and t, u, v, and w are all vectors, prove the following identities using the indicial notation: (1) A:B=Tr( AB' Tr(AB") (2) (txu)(vw) = (t - v)(u w)-(tw)(u v) (3) [t(uxv)]w = (t w)(u v)+ (u - w)(vt)+(v w)(tu)
Step by Step Solution
★★★★★
3.54 Rating (151 Votes )
There are 3 Steps involved in it
Step: 1
Sol Given A B are both Second order ten...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2
Step: 3
Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started
Advanced Engineering Mathematics
Authors: ERWIN KREYSZIG
9th Edition
0471488852, 978-0471488859
