if anyone can help I would really appreciate it!

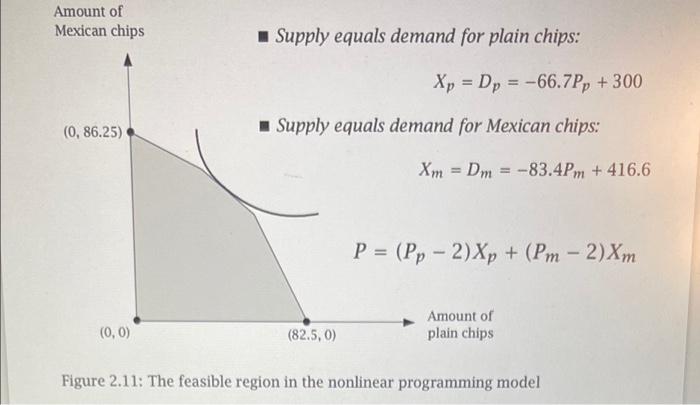
Question 8 (1 point) Listen Consider the nonlinear potato chip production problem discussed in Lectures 6-7 in Week 8, where demand, revenue and profit are given to also depend on price. In class, we had seen that the optimal prices are $3.86 for 1kg of plain chips and $4.26 for 1kg of Mexican chips, for a maximum profit of $218,690. What is the optimal profit or solution returned by Solver when we require prices to be in full dollar amounts (e.g., $1. $2, $3, $4, etc.)? Type your answer in dollars or words. a Maximize: Net profit, Subject to: a time restriction on slicing, a time restriction on frying, a time restriction on packing, and negative amounts cannot be produced. time (min/kg) required for: slicing frying packing net profit contribution (S/kg) plain chips 2 4 4 Mexican availability chips [min] 4 345 5 480 2 330 2 1.5 Table 2.1: Data in the potato chips problem Maximize: Subject to: P = 2Xp + 1.5Xm 2Xp + 4Xm = 345 4Xp + 5Xm s 480 4Xp + 2Xm 3 330 Xp, Xm 20 (slicing) (frying) (packing) Amount of Mexican chips Supply equals demand for plain chips: Xp = Dp = -66.7Pp + 300 (0, 86.25) Supply equals demand for Mexican chips: Xm = Dm = -83.4Pm + 416.6 P = (Pp - 2)Xp + (Pm - 2)Xm (0,0) (82.5, 0) Amount of plain chips Figure 2.11: The feasible region in the nonlinear programming model Question 8 (1 point) Listen Consider the nonlinear potato chip production problem discussed in Lectures 6-7 in Week 8, where demand, revenue and profit are given to also depend on price. In class, we had seen that the optimal prices are $3.86 for 1kg of plain chips and $4.26 for 1kg of Mexican chips, for a maximum profit of $218,690. What is the optimal profit or solution returned by Solver when we require prices to be in full dollar amounts (e.g., $1. $2, $3, $4, etc.)? Type your answer in dollars or words. a Maximize: Net profit, Subject to: a time restriction on slicing, a time restriction on frying, a time restriction on packing, and negative amounts cannot be produced. time (min/kg) required for: slicing frying packing net profit contribution (S/kg) plain chips 2 4 4 Mexican availability chips [min] 4 345 5 480 2 330 2 1.5 Table 2.1: Data in the potato chips problem Maximize: Subject to: P = 2Xp + 1.5Xm 2Xp + 4Xm = 345 4Xp + 5Xm s 480 4Xp + 2Xm 3 330 Xp, Xm 20 (slicing) (frying) (packing) Amount of Mexican chips Supply equals demand for plain chips: Xp = Dp = -66.7Pp + 300 (0, 86.25) Supply equals demand for Mexican chips: Xm = Dm = -83.4Pm + 416.6 P = (Pp - 2)Xp + (Pm - 2)Xm (0,0) (82.5, 0) Amount of plain chips Figure 2.11: The feasible region in the nonlinear programming model