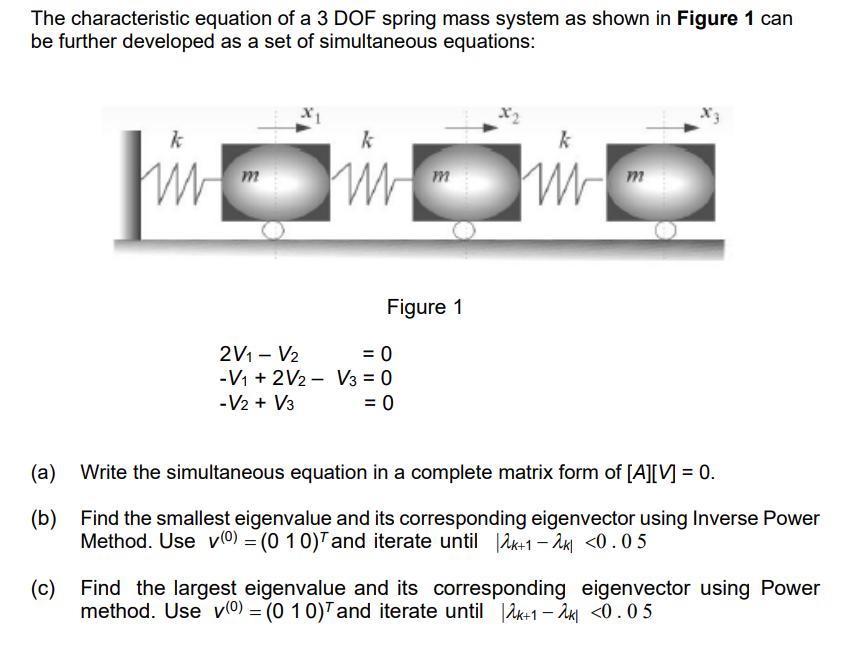
The characteristic equation of a 3 DOF spring mass system as shown in Figure 1 can be further developed as a set of simultaneous equations: k k k m M Figure 1 2V1 V2 = 0 -V1 2V2 V3 = 0 -V2 + V3 = 0 (a) Write the simultaneous equation in a complete matrix form of [A][V]= 0. (b) Find the smallest eigenvalue and its corresponding eigenvector using Inverse Power Method. Use v(0) = (010) and iterate until 2k+1-k