If you answer well I will give you a thumbs up! Please write the code in C++

OUTPUT SHOULD BE:

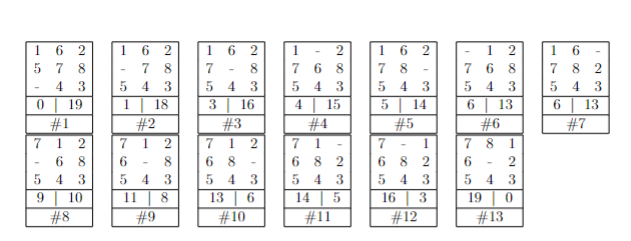
We consider a variant of the 8-puzzle problem (http://tristanpenman. com/demos-puzzle) under a windy condition. The initial state and the goal state are shown as follows: We assume that the wind comes from the north. The step cost regarding the agent's moving a non-blank tile to the neighboring blank tile is defined as follows: 1 for moving southward; 2 for moving westward or eastward; 3 for moving northward. The evaluation function f(n)=g(n)+h(n), where g(n) is the path cost and h(n) is the heuristic function. g(n) is defined as the path cost until the current state n by considering the windy step cost. For h(n), we use a modified total Manhattan distance used in class by considering the windy situation. We define h(n)=i=18hi(n), where hi(n) is for each tile. For example, for the initial node, regarding Tile 8, the agent has to move at least 1-step northward and 1-step westward in order to reach the goal. Therefore, we have h8(n)=31+21=5 at the initial state. In your implementation, please use a priority queue for the frontier and a hash table for the expored set. The priority is based on the evaluation function f(n). The smaller the value, the higher the priority. When adding children to an expansion node, use such order of moving the non-blank tile to the neighboring blank tiles: first the west neighboring non-blank tile; then north one; then the east one; then the south one. To break tie in picking an expansion node, use FIFO order. In your testing output, please print out all expansion states in the sequence as shown on next page: For the printout of each state, the last 2nd row includes g(n) value at the left and h(n) value at the right, and the last row indicates the expansion order. Note: this printout is the expansion order, not the actual optimal path. \begin{tabular}{|ccc|} \hline 1 & 6 & 2 \\ 5 & 7 & 8 \\ & 4 & 3 \\ \hline 0 & & 19 \\ \hline \multicolumn{3}{|c|}{#1} \\ \hline 7 & 1 & 2 \\ & 6 & 8 \\ 5 & 4 & 3 \\ \hline 9 & \multicolumn{1}{|c|}{10} \\ \hline \multicolumn{3}{|c|}{#8} \\ \hline \end{tabular} \begin{tabular}{|ccc|} \hline 1 & 6 & 2 \\ & 7 & 8 \\ 5 & 4 & 3 \\ \hline 1 & 1 & 18 \\ \hline \multicolumn{3}{|c|}{#2} \\ \hline 7 & 1 & 2 \\ 6 & & 8 \\ 5 & 4 & 3 \\ \hline 11 & 1 & 8 \\ \hline \multicolumn{3}{|c|}{#9} \\ \hline \end{tabular} \begin{tabular}{|lll|} \hline 1 & 6 & 2 \\ 7 & & 8 \\ 5 & 4 & 3 \\ \hline 3 & \multicolumn{1}{|c|}{16} \\ \hline \multicolumn{3}{|c|}{#3} \\ \hline 7 & 1 & 2 \\ 6 & 8 & \\ 5 & 4 & 3 \\ \hline 13 & 6 \\ \hline# & 6 \\ \hline \end{tabular} \begin{tabular}{|lll|} \hline 1 & & 2 \\ 7 & 6 & 8 \\ 5 & 4 & 3 \\ \hline 4 & \multicolumn{1}{|c|}{15} \\ \hline \multicolumn{3}{|c|}{#} \\ \hline 7 & 1 & \\ 6 & 8 & 2 \\ 5 & 4 & 3 \\ \hline 14 & 5 \\ \hline#11 \\ \hline \end{tabular} \begin{tabular}{|lll|} \hline 1 & 6 & 2 \\ 7 & 8 & \\ 5 & 4 & 3 \\ \hline 5 & \multicolumn{1}{|c|}{14} \\ \hline \multicolumn{3}{|c|}{#5} \\ \hline 7 & & 1 \\ 6 & 8 & 2 \\ 5 & 4 & 3 \\ \hline 16 & 3 \\ \hline# & & 32 \\ \hline \end{tabular} \begin{tabular}{|lll|} \hline & 1 & 2 \\ 7 & 6 & 8 \\ 5 & 4 & 3 \\ \hline 6 & & 13 \\ \hline \multicolumn{3}{|c|}{#6} \\ \hline 7 & 8 & 1 \\ 6 & & 2 \\ 5 & 4 & 3 \\ \hline 19 & 0 \\ \hline# & 13 \\ \hline \end{tabular} \begin{tabular}{|ccc|} \hline 1 & 6 & \\ 7 & 8 & 2 \\ 5 & 4 & 3 \\ \hline 6 & \multicolumn{2}{c|}{13} \\ \hline \multicolumn{3}{|c|}{#7} \\ \hline \end{tabular}