I'm having difficulties implementing this with utilizing Iterator, any help is greatly appreciated.

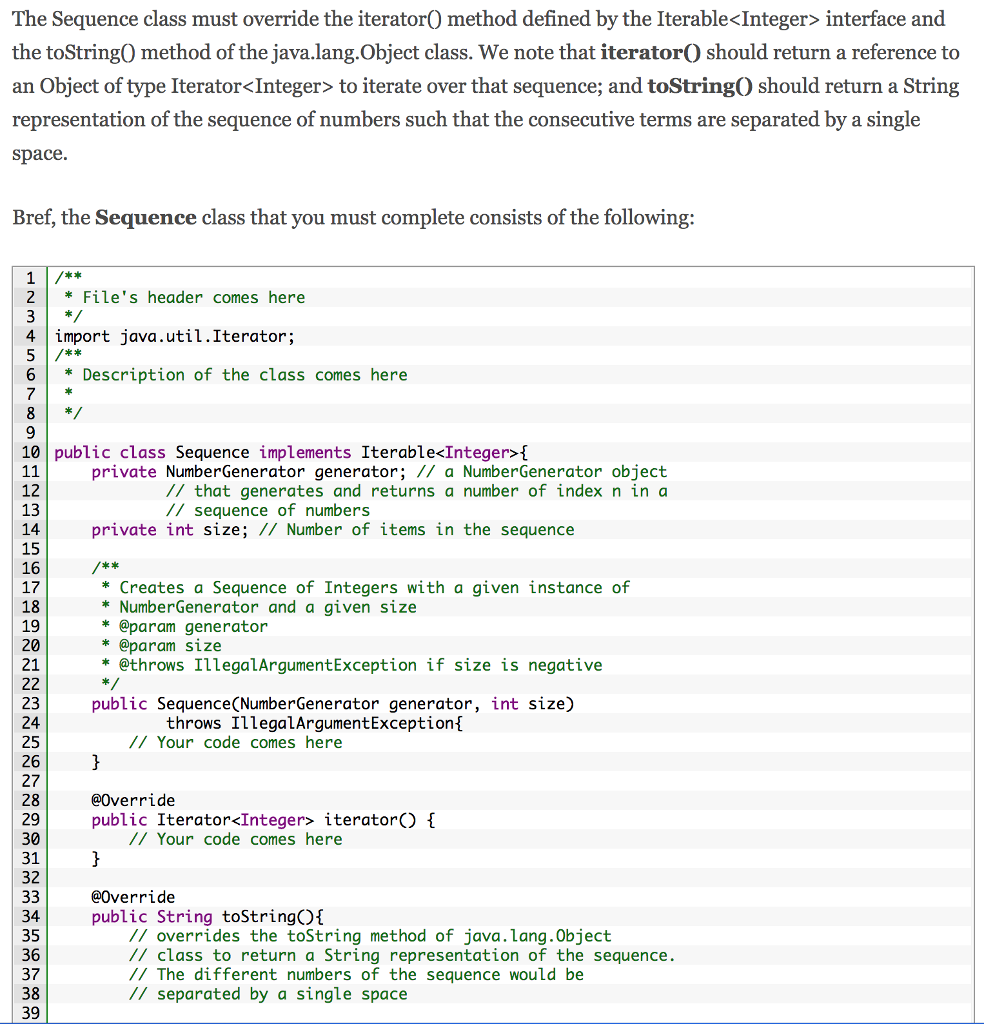
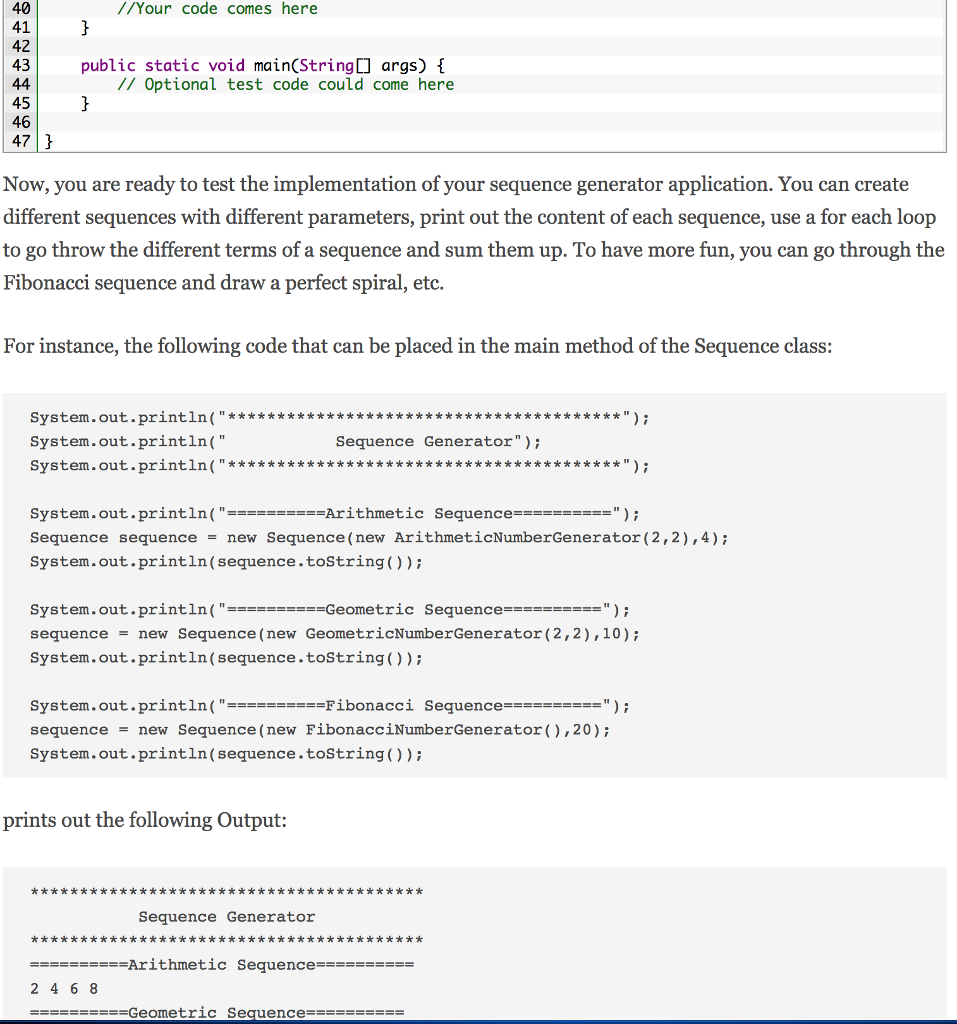
INTRODUCTION To get started, you should have a clear idea of what is a numeric progression. Recall that a numeric progression is a sequence of numbers, where each number depends on one or more of the previous numbers. In general, a progression requires to define a first value, and a way to identify a new value (next value) based on one or more previous values. For instance, an arithmetic progression is a sequence of numbers such that the difference between the consecutive values is constant. In other terms, the next number is determined by adding a fixed constant (aka common difference) to the previous value. For example, the sequence 5, 7, 9, 11, 13, 15, is an arithmetic progression with first term 5 and common difference of 2. a geometric progression determines the next number by multiplying the previous value by a fixed constant (aka common ratio). For instance, the sequence 3, 6, 12, 24, 48, is a geometric progressiorn with first term 3 and common ratio of 2. a Fibonacci progression determines the next number by summing the two most recent previous values. To start the sequence, the first two values are conventionally o and 1, leading to the Fibonacci sequence: o, 1, 1, 2, 3, 5, 8, More generally, such a sequence can be generated from any two starting values. For instance, the sequence 4, 6, 10, 16, 26, 42,... is a Fibonacci progression with starting values 4 and 6. Written as a rule, the expression is xn - Xn-1 + Xn-2- CREATE A SEQUENCE GENERATOR The goal of this first part of the assignment is to build a sequence generator program for iterating numeric sequences. First, you will create a hierarchy of classes to generate numbers for number progression sequences: a NumberGenerator interface and three classes ArithmeticNumberGenerator, GeometricNumberGenerator, and FibonacciNumberGenerator that implement that interface. Then, you will create two classes: an iterable Sequence class that represents any numerical progression and a Sequencelterator class that iterates over any sequence of numbers