I'm having trouble calling the previous function and inputting my new values...

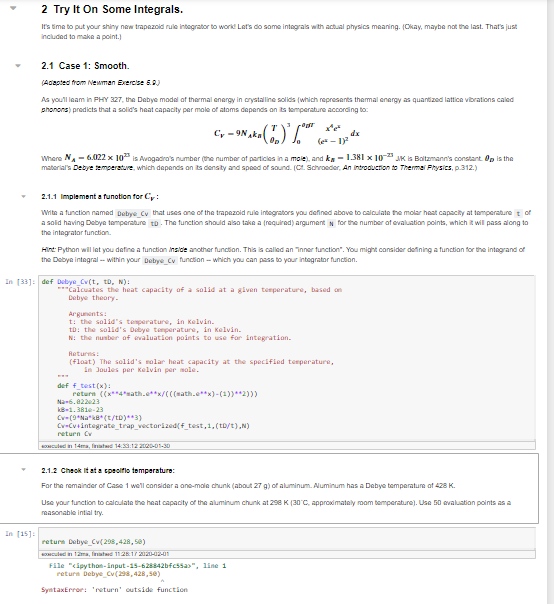
2 Try It On Some Integrals. It's time to put your shiny new trapezoid rule integrator to worid Let's do some integrals with actual physics meaning. Okay, maybe not the last. That's just included to make a point.) 2.1 Case 1: Smooth (Adapted from Newman Exercise 5.2) As you'll leam in PHY 327, the Debye model of thermal energy in crystalline solids which represents themal energy as quantized lattice vibrations caled Shonons predicts that a solid's heat capacity per mole of atoms depends on its temperature according to C -9N, 1. (-18 Where N -6.022 x 10is Avogadro's number the number of particles in a mole,and k -1.381 x 10- JK IS Boltzmann's constant. Op is the material's Debye temperature, which depends on its density and speed of sound. Schroeder Annoueronto Thermal Physics, p. 312.) 2.1.1 Implement a function for Cr: Write a function named Debye Cy that uses one of the trapezoid rule integrators you defined above to calculate the molar heat capacity at temperature of a solid having Debye temperature to. The function should also take a required) argument for the number of evaluation points, which will pass along to the integrator function Hind: Python will let you define a function inside another function. This is called an inner function". You might consider defining a function for the integrand of the Debye integral -- within your Debye Cy function which you can pass to your integrator function. In 33)def Debye CV(t, tb, N): **Calcuates the heat capacity of a solid at a given temperature, based on Debye theory to the solid's temperature, in Kelvin. TD: the solid's Debye temperature in Kelvin. N: the number of evaluation points to use for integration. (float) The solid's molar heat capacity at the specified temperature, in Joules per kelvin per mole. def + test(x): return (x4eath.e**x/(((math.e***)-(1))*2))) Cv (9'Na'kB (t/tD) ) Cv-Cv4integrate_trap_vectorized(f_test,1.(t/t).N) 2.1.2 Check it at a cpsoillo temperature: For the remainder of Case 1 we'll consider a one-mole chunk (about 27 g) of aluminum Numinum has a Debye temperature of 428 K. Use your function to calculate the heat capacity of the aluminum chunk at 298 K (30C, approximately room temperature). Use 50 evaluation points as a reasonable intialtry. In 15) returi Debye CV 298,428,50) culum , 112.17 22-02-01 File "