im quite confused on this loop invariant thing. i know how to algorithm for insertion sort runs however the loop invariant A[1...j-1] etc confuse me. the three properties are (initialization, maintenance, terminarion). here are pics

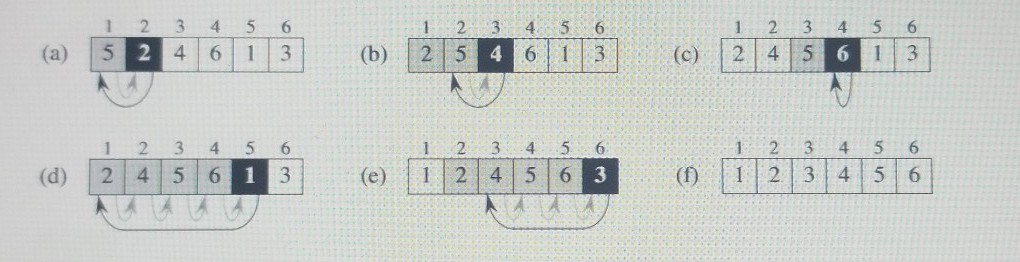
5 6 1 2 3 4 5246| 23 45 25 46 1| 2 4 3 5 4 6 5 1| 2 1 2 3 4 5 6 2456 13 2 3 4 5 6 | 124563 2 3 4 5 6 0 123 lols456 anno INSERTION-SORT(A) 1 for j = 2 to A. length key = A[] // Insert A[j] into the sorted sequence A[1.. j - 1]. i = j-1 while i > 0 and A[i] > key A[i + 1] = A[i] i = 1 - 1 Ali + 1] = key Initialization: We start by showing that the loop invariant holds before the first loop iteration, when j = 2.' The subarray All.. j - 1], therefore, consists of just the single element A[1], which is in fact the original element in A[1]. Moreover, this subarray is sorted (trivially, of course), which shows that the loop invariant holds prior to the first iteration of the loop. Maintenance: Next, we tackle the second property: showing that each iteration maintains the loop invariant. Informally, the body of the for loop works by moving Alj - 1], AL -2), A[j - 3], and so on by one position to the right until it finds the proper position for Ajl (lines 4-7), at which point it inserts the value of All (line 8). The subarray Al.. jl then consists of the elements originally in A[1.j, but in sorted order. Incrementing j for the next iteration of the for loop then preserves the loop invariant. A more formal treatment of the second property would require us to state and show a loop invariant for the while loop of lines 5-7. At this point, however, we prefer not to get bogged down in such formalism, and so we rely on our informal analysis to show that the second property holds for the outer loop. Termination: Finally, we examine what happens when the loop terminates. The condition causing the for loop to terminate is that j > A.length = n. Because each loop iteration increases by 1, we must have j = n + 1 at that time. Substituting n + 1 for j in the wording of loop invariant, we have that the subarray A[1..n) consists of the elements originally in A[1..n], but in sorted order. Observing that the subarray A[1..n] is the entire array, we conclude that the entire array is sorted. Hence, the algorithm is correct. We shall use this method of loop invariants to show correctness later in this chapter and in other chapters as well