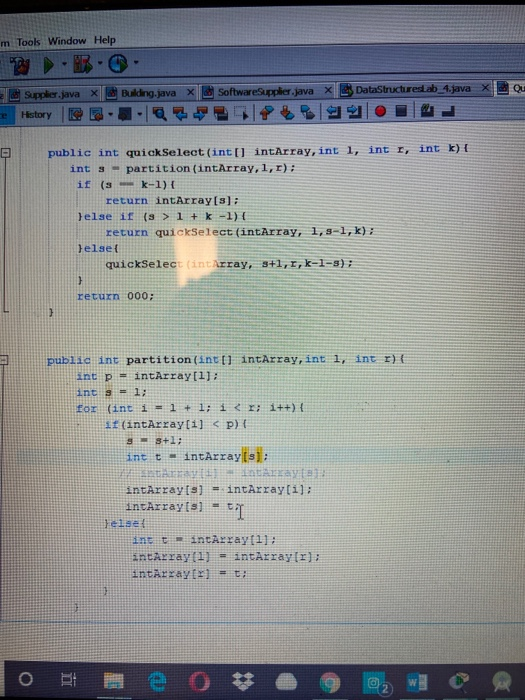
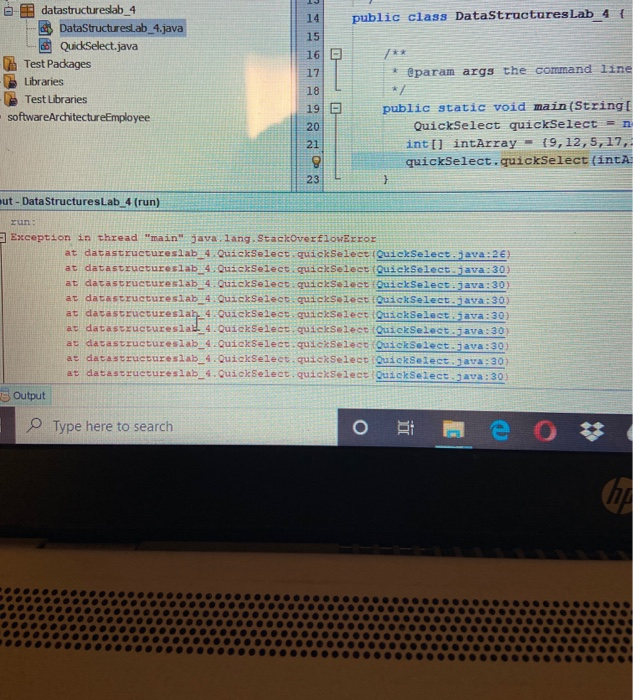
im trying to write this code but i am getting this error as an output. i gues im swapping it wrongly or so?
public class QuickSelect {
//in the quickselect class, we will write the partition algorithm
//int[] intArray = {9,12,5,17,20,30,8};
// int p = intArray[0];
// int s = 0;
// int k = (intArray.length) / 2;
QuickSelect(){
}
public int quickSelect(int[] intArray,int l, int r, int k){
int s = partition(intArray,l,r);
if (s == k-1){
return intArray[s];
}else if (s > l + k -1){
return quickSelect(intArray, l,s-1,k);
}else{
quickSelect(intArray, s+1,r,k-1-s);
}
return 000;
}
public int partition(int[] intArray,int l, int r){
int p = intArray[l];
int s = l;
for (int i = l + 1; i
if(intArray[i]
s = s+1;
int t = intArray[s];
// intArray[i] = intArray[s];
intArray[s] = intArray[i];
intArray[s] = t;
}else{
int t = intArray[l];
intArray[l] = intArray[r];
intArray[r] = t;
}
}
return s;
}
}
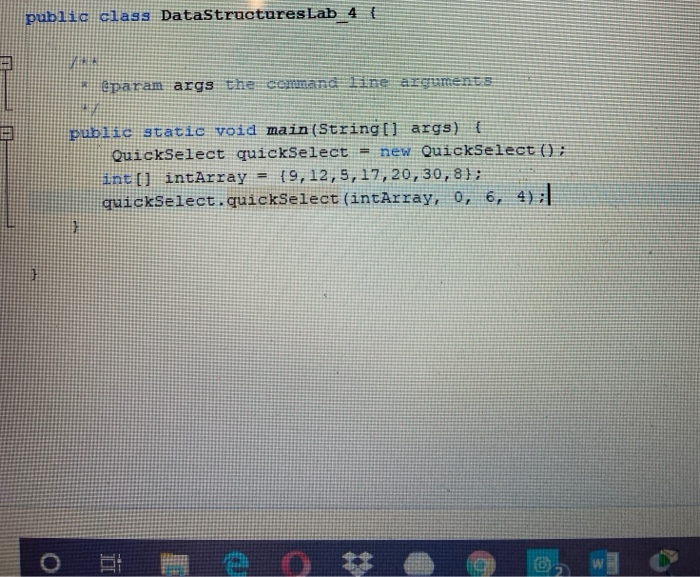
public class DataStructuresLab_4 {
/**
* @param args the command line arguments
*/
public static void main(String[] args) {
QuickSelect quickSelect = new QuickSelect();
int[] intArray = {9,12,5,17,20,30,8};
quickSelect.quickSelect(intArray, 0, 6, 4);
}
}
P154 ALGORITHM Lomo Partition(All...]) Martitions subarray by Lomuto's algorithm using first element as pivot Input: A subarray A[...] of array AfO..-1). defined by its left and righi 1/ indices/andr (lar) I/Output: Partition of All...) and the new position of the pivot PA[ for i + I tor do if Ali]
-1, the kth smallest element in the entire array can be found us the kth smallest element in the left part of the partitioned array. And ifs I+*-1 Quickselect(A1.5 - 1). 4) else Quickselect(Als + r). - 1 - 3) In fact, the sume idea can be implemented without recursion as well. For the nonrecursive version, we need nal even adjust the value of a but just continue until s =k-1. m Tools Window Help Building java X X Suppler.javax History SoftwareSuppler.java P DataStructures ab_4.java M public int quickSelect(int intArray, int i, int i, int k) int 3 - partition (intArray,1,1); if ( k-1) { return intArray[3]; }else if (s > 1+ k-1) { return quickSelect (intArray, 1,9-1,k); Helset quickSelect (intArray, 3+1, 1, k-1-3); return 000; public int partition (int[] intArray, int i, int I) int p = intArray[1]: for (int i = 1 + 1; i