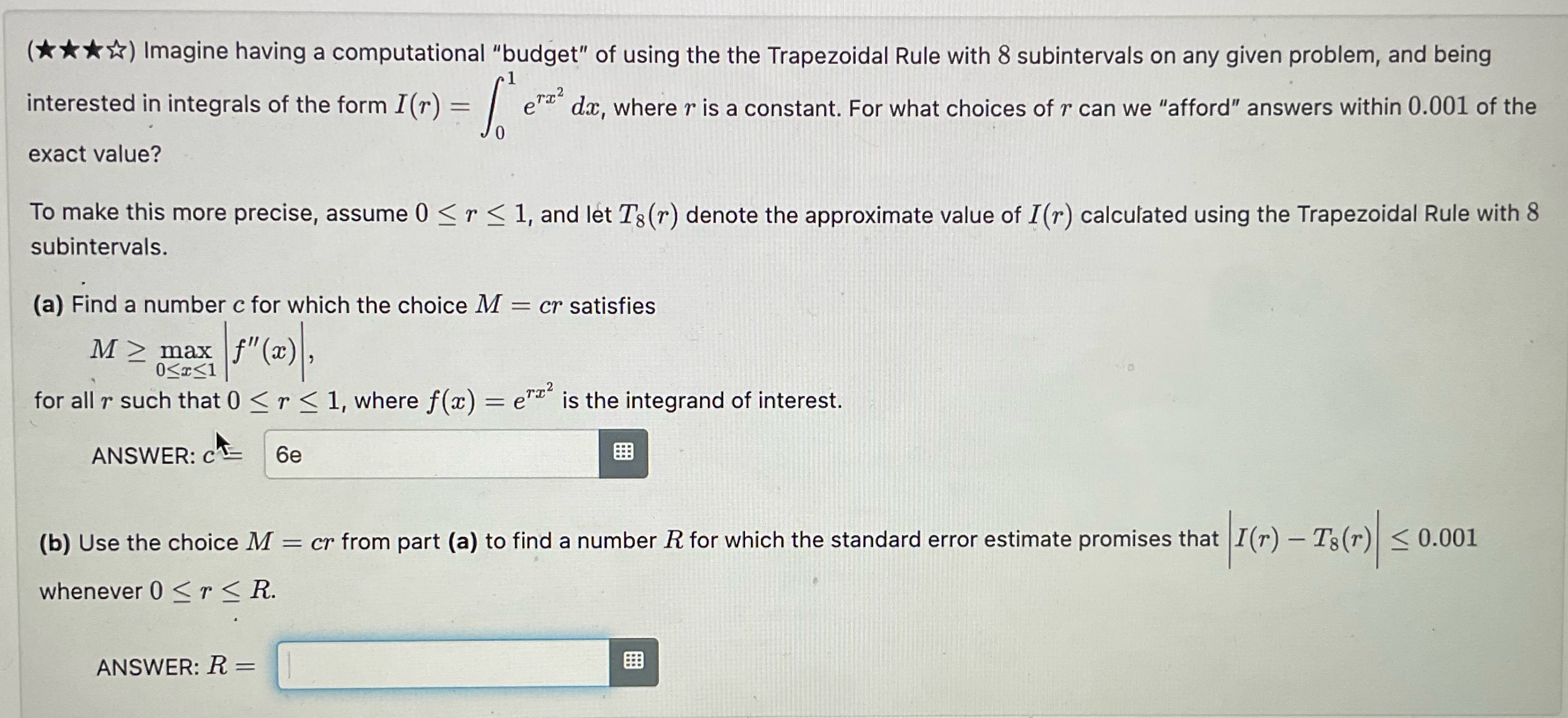
() Imagine having a computational "budget" of using the the Trapezoidal Rule with 8 subintervals on any given problem, and being interested in integrals of the form I (r) = ( e dar, where r is a constant. For what choices of r can we "afford" answers within 0.001 of the exact value? To make this more precise, assume 0 < r < 1, and let Ts (r) denote the approximate value of I(r) calculated using the Trapezoidal Rule with 8 subintervals. (a) Find a number c for which the choice M = cr satisfies M> max 0x1 "(x), for all r such that 0 < r < 1, where f(x) = e is the integrand of interest. ANSWER: c 6e (b) Use the choice M = cr from part (a) to find a number R for which the standard error estimate promises that I (r) - T&(r)| whenever 0