Implement a stack and solutions to the following problems: balancing parenthesis, evaluating postfix expressions and transforming infix expressions into postfix expressions.

We are providing some sample code and input files:

public/

balancing.cpp

-main method to check whether an expression is balanced

infix2postfix.cpp

-main method to transform an infix expression into postfix input_balanced.txt

-test cases for balancing.cpp

input_infix2postfix.txt

-test cases for infixtopostfix.cpp

input_postfixEval.txt

-test cases for postfixEval.cpp

postfixEval.cpp

-main method to evaluate postfix expressions

stack.cpp

-stack implementation

stack.hpp

-stack header file

To compile,

run$ g++ stack.cpp balancing.cpp $ g++stack.cpp postfixEval.cpp $ g++stack.cpp infixtopostfix.cpp

To run each program, run$ ./a.out

The test cases follow this format: expected_solution input. Given input, your job is to implement code that gets the expected_solution. Obviously, you need to calculate expected_solution, notjust print it. balancing.cppmustbalance round parentheses, and square and curly brackets (()[]{}) While we provide a few test cases, you are expected to add more to make sure your code works

Transform postfix expressions into infix expressions. Evaluate postfix expressions when the operands can be any number (not only one digit). The easiest way to do this is to use whitespace as a delimiter. Transform infix expressions into postfix, but also allow for the sign operator (). The code we say in classassumes that all operators are binary, but the sign operator is unary, e.g., (24).

stackcpp

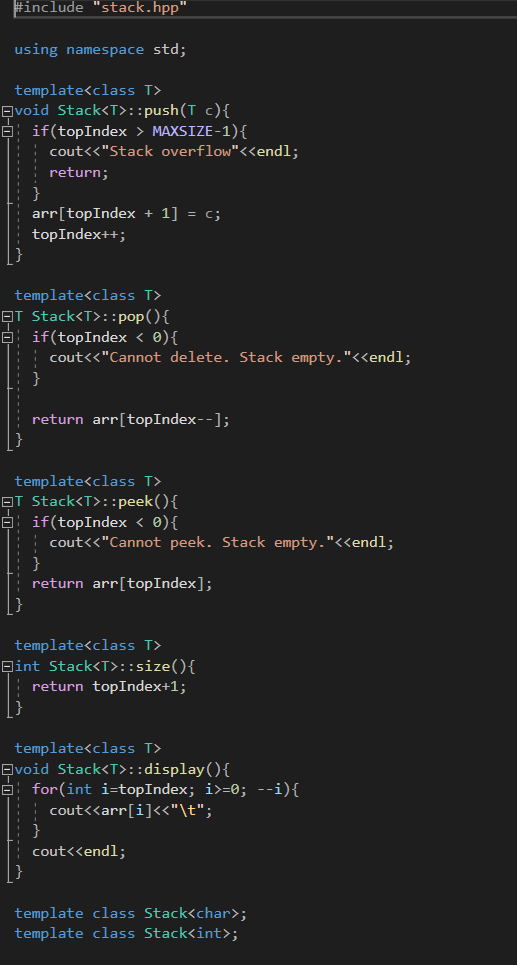
stackhpp

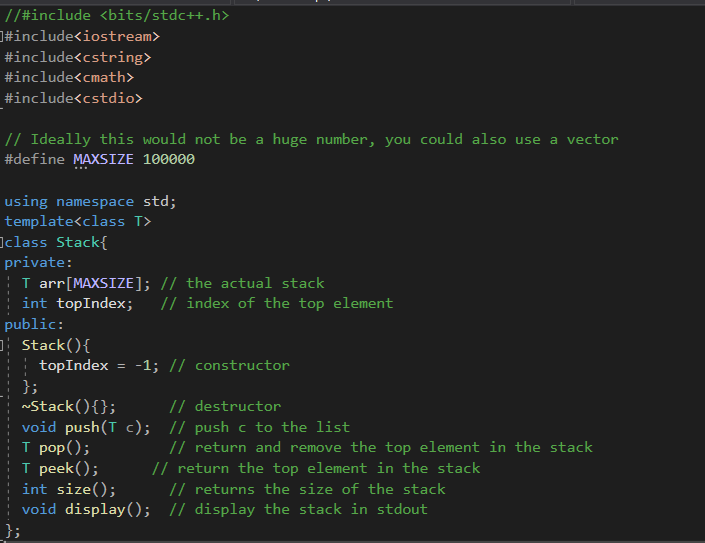
infix2postfix

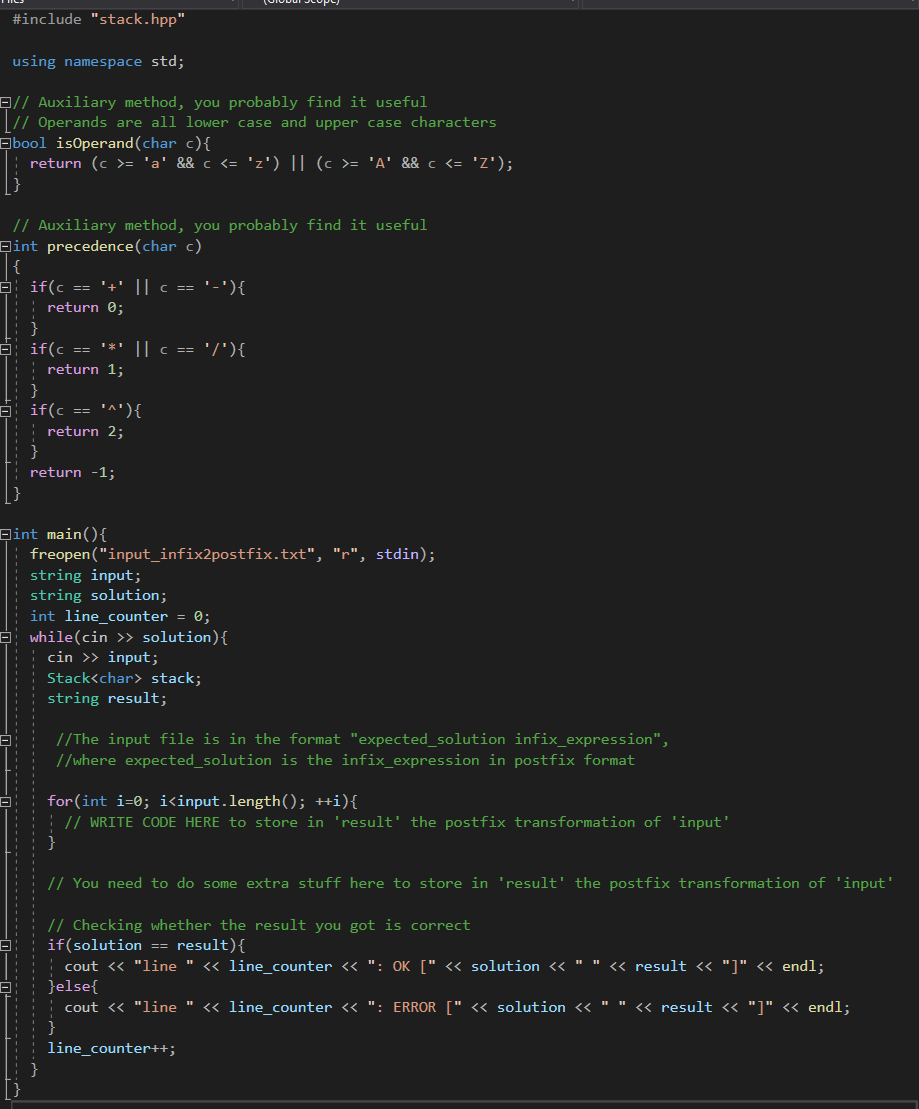
postfixevaluation

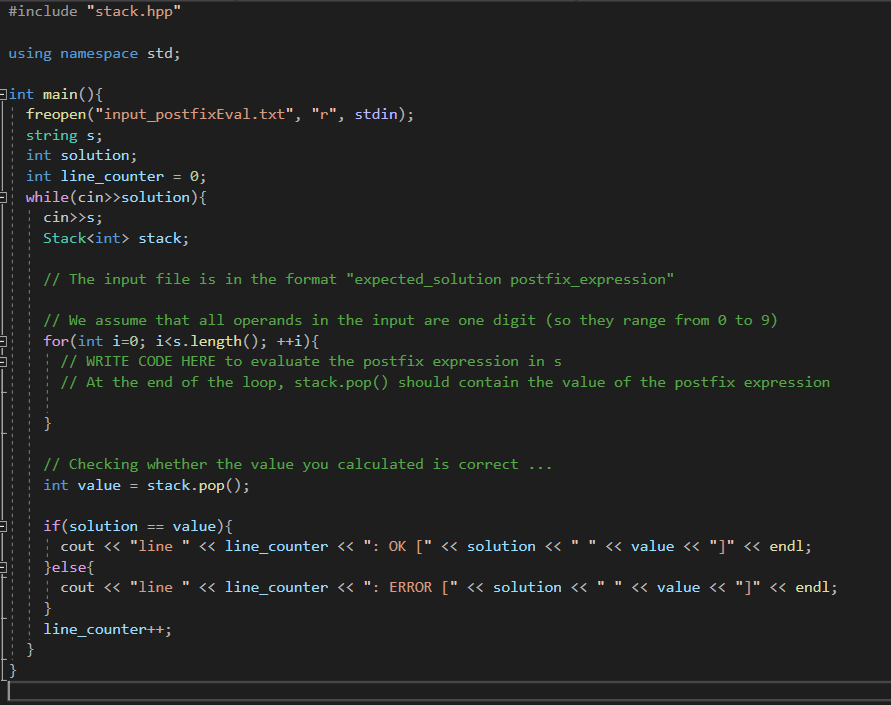
balancing

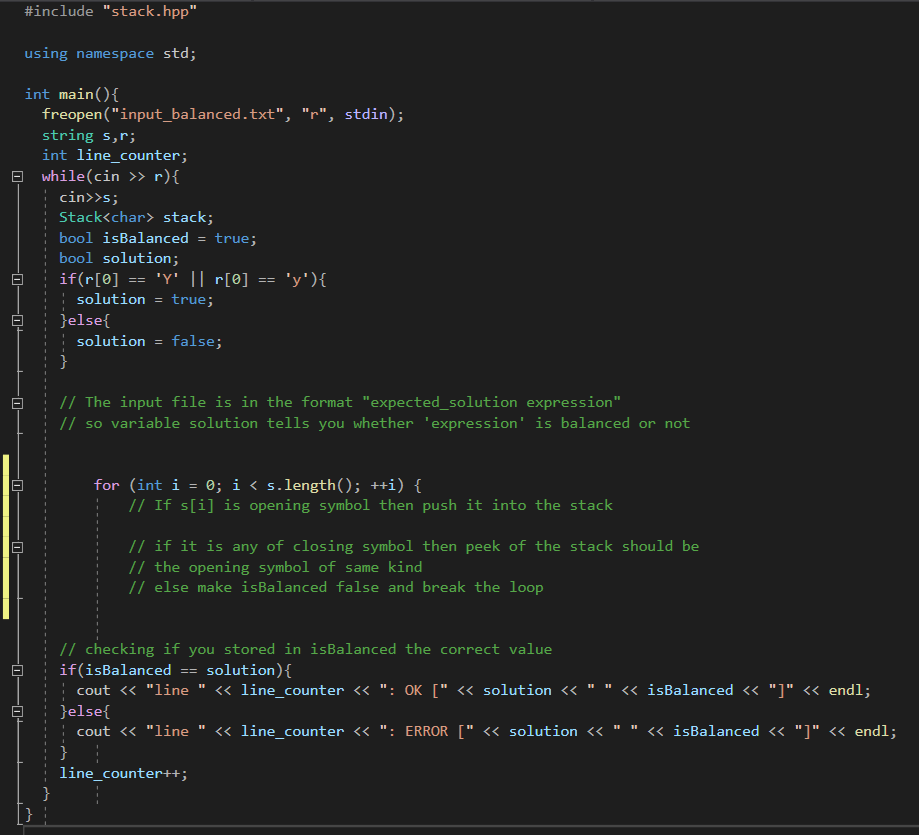
stack.cpp

#include "stack.hpp"

using namespace std;

template void Stack::push(T c){ if(topIndex > MAXSIZE-1){ cout

template T Stack::pop(){ if(topIndex

return arr[topIndex--]; }

template T Stack::peek(){ if(topIndex

template int Stack::size(){ return topIndex+1; }

template void Stack::display(){ for(int i=topIndex; i>=0; --i){ cout

template class Stack; template class Stack;

stackhpp

//#include #include #include #include #include

// Ideally this would not be a huge number, you could also use a vector #define MAXSIZE 100000

using namespace std; template class Stack{ private: T arr[MAXSIZE]; // the actual stack int topIndex; // index of the top element public: Stack(){ topIndex = -1; // constructor }; ~Stack(){}; // destructor void push(T c); // push c to the list T pop(); // return and remove the top element in the stack T peek(); // return the top element in the stack int size(); // returns the size of the stack void display(); // display the stack in stdout };

infix2postfix

#include "stack.hpp"

using namespace std;

// Auxiliary method, you probably find it useful // Operands are all lower case and upper case characters bool isOperand(char c){ return (c >= 'a' && c = 'A' && c

// Auxiliary method, you probably find it useful int precedence(char c) { if(c == '+' || c == '-'){ return 0; } if(c == '*' || c == '/'){ return 1; } if(c == '^'){ return 2; } return -1; }

int main(){ freopen("input_infix2postfix.txt", "r", stdin); string input; string solution; int line_counter = 0; while(cin >> solution){ cin >> input; Stack stack; string result;

//The input file is in the format "expected_solution infix_expression", //where expected_solution is the infix_expression in postfix format

for(int i=0; i

postfixevaluation

#include "stack.hpp"

using namespace std;

int main(){ freopen("input_postfixEval.txt", "r", stdin); string s; int solution; int line_counter = 0; while(cin>>solution){ cin>>s; Stack stack; // The input file is in the format "expected_solution postfix_expression"

// We assume that all operands in the input are one digit (so they range from 0 to 9) for(int i=0; i

// Checking whether the value you calculated is correct ... int value = stack.pop();

if(solution == value){ cout

balancing

#include "stack.hpp"

using namespace std;

int main(){ freopen("input_balanced.txt", "r", stdin); string s,r; int line_counter; while(cin >> r){ cin>>s; Stack stack; bool isBalanced = true; bool solution; if(r[0] == 'Y' || r[0] == 'y'){ solution = true; }else{ solution = false; }

// The input file is in the format "expected_solution expression" // so variable solution tells you whether 'expression' is balanced or not

for(int i=0; i

// checking if you stored in isBalanced the correct value if(isBalanced == solution){ cout

#include "stack.hpp" using namespace std; template void Stack:: push(T c){ if(topIndex > MAXSIZE-1){ cout T Stack::pop(){ if(topIndex AT Stack:: peek() { if(topIndex Qint Stack::size(){ return topIndex+1; template Ivoid Stack::display(){ for(int i=topIndex; i>=0; --i){ cout; template class Stack int>; //#include #include #include #include #include // Ideally this would not be a huge number, you could also use a vector #define MAXSIZE 100000 using namespace std; template class Stack{ private: I arr[MAXSIZE]; // the actual stack int topIndex; // index of the top element public: ) Stack(){ topIndex -1; // constructor }; Stack(){}; // destructor void push(T c); // push c to the list I pop(); // return and remove the top element in the stack I peek(); // return the top element in the stack int size(); // returns the size of the stack void display(); // display the stack in stdout }; #include "stack.hpp" using namespace std; // Auxiliary method, you probably find it useful // Operands are all lower case and upper case characters qbool isoperand(char c){ return ( >= 'a' && = 'A' && > solution) { cin >> input; Stack stack; string result; [/The input file is in the format "expected_solution infix_expression", 1/where expected_solution is the infix_expression in postfix format for(int i=0; i>solution) { cin>>s; Stack stack; // The input file is in the format "expected_solution postfix_expression" // We assume that all operands in the input are one digit (so they range from 0 to 9) for(int i=0; i> r){ cin>>s; Stack stack; bool isBalanced true; bool solution; if(r[@] == 'Y' || r[@] 'y'){ solution = true; }else{ solution = false; } . == // The input file is in the format "expected_solution expression" // so variable solution tells you whether 'expression' is balanced or not for (int i = 0; i void Stack:: push(T c){ if(topIndex > MAXSIZE-1){ cout T Stack::pop(){ if(topIndex AT Stack:: peek() { if(topIndex Qint Stack::size(){ return topIndex+1; template Ivoid Stack::display(){ for(int i=topIndex; i>=0; --i){ cout; template class Stack int>; //#include #include #include #include #include // Ideally this would not be a huge number, you could also use a vector #define MAXSIZE 100000 using namespace std; template class Stack{ private: I arr[MAXSIZE]; // the actual stack int topIndex; // index of the top element public: ) Stack(){ topIndex -1; // constructor }; Stack(){}; // destructor void push(T c); // push c to the list I pop(); // return and remove the top element in the stack I peek(); // return the top element in the stack int size(); // returns the size of the stack void display(); // display the stack in stdout }; #include "stack.hpp" using namespace std; // Auxiliary method, you probably find it useful // Operands are all lower case and upper case characters qbool isoperand(char c){ return ( >= 'a' && = 'A' && > solution) { cin >> input; Stack stack; string result; [/The input file is in the format "expected_solution infix_expression", 1/where expected_solution is the infix_expression in postfix format for(int i=0; i>solution) { cin>>s; Stack stack; // The input file is in the format "expected_solution postfix_expression" // We assume that all operands in the input are one digit (so they range from 0 to 9) for(int i=0; i> r){ cin>>s; Stack stack; bool isBalanced true; bool solution; if(r[@] == 'Y' || r[@] 'y'){ solution = true; }else{ solution = false; } . == // The input file is in the format "expected_solution expression" // so variable solution tells you whether 'expression' is balanced or not for (int i = 0; i