Implement the following algorithm strongly connected components algorithm in python:

Given a directed graph G you first create the reverse graph GR in linear time. Next, you run the undirected connected components method from sec 3.2.3, processing the vertices in decreasing post order. You must make sure that both steps can be carried out in O(|V|+|E|) time. In more detail, carry out the following steps:

1. Create GR

2. Compute DFS interval on GR for each node

3. Iteratively select the next unvisited node uu with highest post(u)post(u):

For each such u, use DFS on G to visit all nodes reachable from u and output this set as a connected component.

Your python script should read the graph file name from the command line. Each line of the graph file will have two integers representing a directed edge from u to v. You code should output all strongly connected components.

You cannot use any external python graph library. Do not implement an elaborate graph class either. Just use the adjacency list format to store the input graph. Make sure not to use sorting, otherwise the time will not be linear. You may need to increase the maximum recursion depth via the sys.setrecursionlimit call

PLEASE VERIFY IT WORKS BY RUNNING A TEXT FILE WITH THE FOLLOWING CONTENTS: 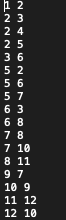THE OUT PUT SHOULD BE SIMILAR TO:

1. Run depth-first search on GR. 2. Run the undirected connected components algorithm (from Section 3.2.3) on G, and during the depth-first search, process the vertices in decreasing order of their post numbers from step 1. 3.2.3 Connectivity in undirected graphs These regions are called connected components: each of them is a subgraph that is internally connected but has no edges to the remaining vertices. When explore is started at a particular vertex, it identifies precisely the connected component containing that vertex. And each time the DFS outer loop calls explore, a new connected component is picked out. Thus depth-first search is trivially adapted to check if a graph is connected and, more generally, to assign each node v an integer ccnum [v] identifying the connected component to which it belongs. All it takes is procedure previsit (v) ccnum[v]=cc where cc needs to be initialized to zero and to be incremented each time the DFS procedure calls explore. 12223555667789101112234562673881011791210 7891011124 36 25 Note that 4 can also come before 789101112