Implement the following in Python!

Code will all be tested with the following: (comments are expected results)

y = 6.5 subMin = np.nextafter(0,1) #subMin = 5e-324 print(sign(y)) #1 print(sign(0.0)) # 0 print(sign(-y)) #-1 print(sign(-0.0)) #0 print(exponent(y)) #2

print(exponent(16.6)) #4 print(fraction(0.0)) #0.0 print(mantissa(y)) #1.625 print(mantissa(0.0) #0.0 var1 = float(nan) print(exponent(var1)) #1024 print(exponent(0.0) #0 print(exponent(subMin)) #-1022 print(is_posinfinity(math.inf)) #True print(is_neginfinity(math.inf)) #False print(not is_posinfinity(-math.inf)) #True print(is_neginfinity(-math.inf)) #True print(ulp(y)) #8.881784197001252e-16 print(ulp(1.0)) #2.220446049250313e-16 print(ulp(0.0)) #5e-324 print(ulp(subMin)) #5e-324 print(ulp(1.0e15)) #0.125 print(ulps(1,2)) #4503599627370496

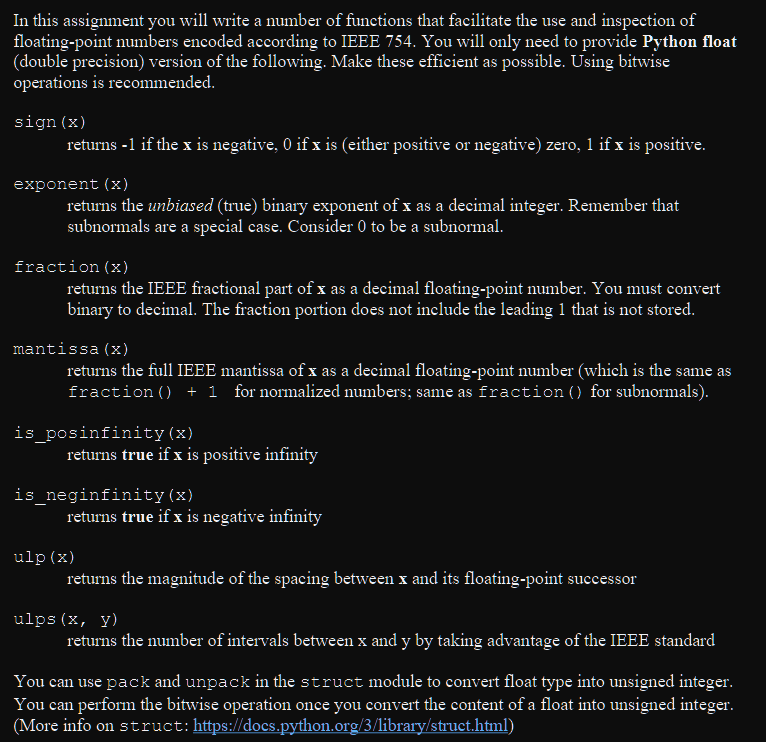
In this assignment you will write a number of functions that facilitate the use and inspection of floating-point numbers encoded according to IEEE 754. You will only need to provide Python float (double precision) version of the following. Make these efficient as possible. Using bitwise operations is recommended. sign(x) returns 1 if the x is negative, 0 if x is (either positive or negative) zero, 1 if x is positive. exponent (x) returns the unbiased (true) binary exponent of x as a decimal integer. Remember that subnormals are a special case. Consider 0 to be a subnormal. fraction (x) returns the IEEE fractional part of x as a decimal floating-point number. You must convert binary to decimal. The fraction portion does not include the leading 1 that is not stored. mantissa(x) returns the full IEEE mantissa of x as a decimal floating-point number (which is the same as fraction () +1 for normalized numbers; same as fraction () for subnormals). is_posinfinity (x) returns true if x is positive infinity is_neginfinity (x) returns true if x is negative infinity ulp(x) returns the magnitude of the spacing between x and its floating-point successor ulps(x,y) returns the number of intervals between x and y by taking advantage of the IEEE standard You can use pack and unpack in the struct module to convert float type into unsigned integer. You can perform the bitwise operation once you convert the content of a float into unsigned integer