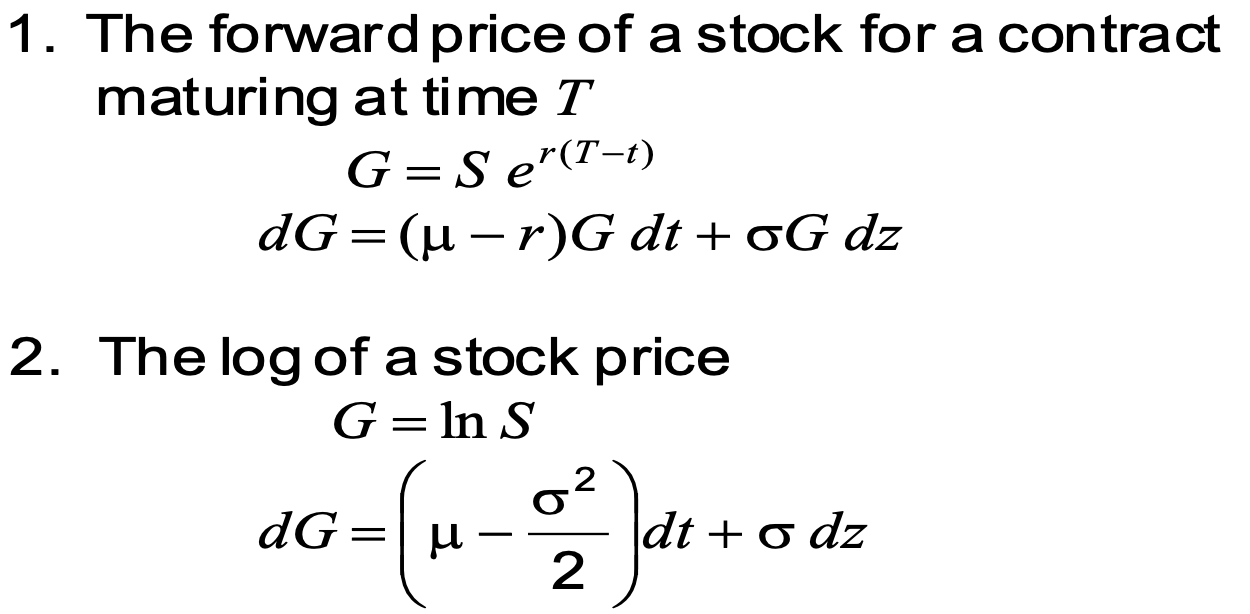
Implication of 2:

Integrate with respect to t, we have S(t)=S(0)(22)+e^((-^2/2)t+t)

We can use this formula to simulate S at any future time t

Under risk neutral environment, we set expected grow rate =r

Select two problems below and turn in your work.

1. Given G(S, t) = 1 "1. Given G(S, t) = " 1/(S ) , prove =2 dG=-(-^2 )G dt-G dz 2. Given G(S, t) = 2"2. Given G(S, t) = " S^2, prove dG = (2 + 2^2)G dt + 2 G dz

3. Given G(S, t) = 2 3t^2 S^3, prove dG = (3 + 2 +322/(t )+3^2)G dt+3 G dz

4. Given G(S, t) = 2t^2, prove dG = 2t dt, a deterministic process

1. The forward price of a stock for a contract maturing at time T G = S er(T-1) dG=(u r)G dt + OG dz 2. The log of a stock price G = ln S 2 dG= ua -(u - dt + o dz 1. The forward price of a stock for a contract maturing at time T G = S er(T-1) dG=(u r)G dt + OG dz 2. The log of a stock price G = ln S 2 dG= ua -(u - dt + o dz