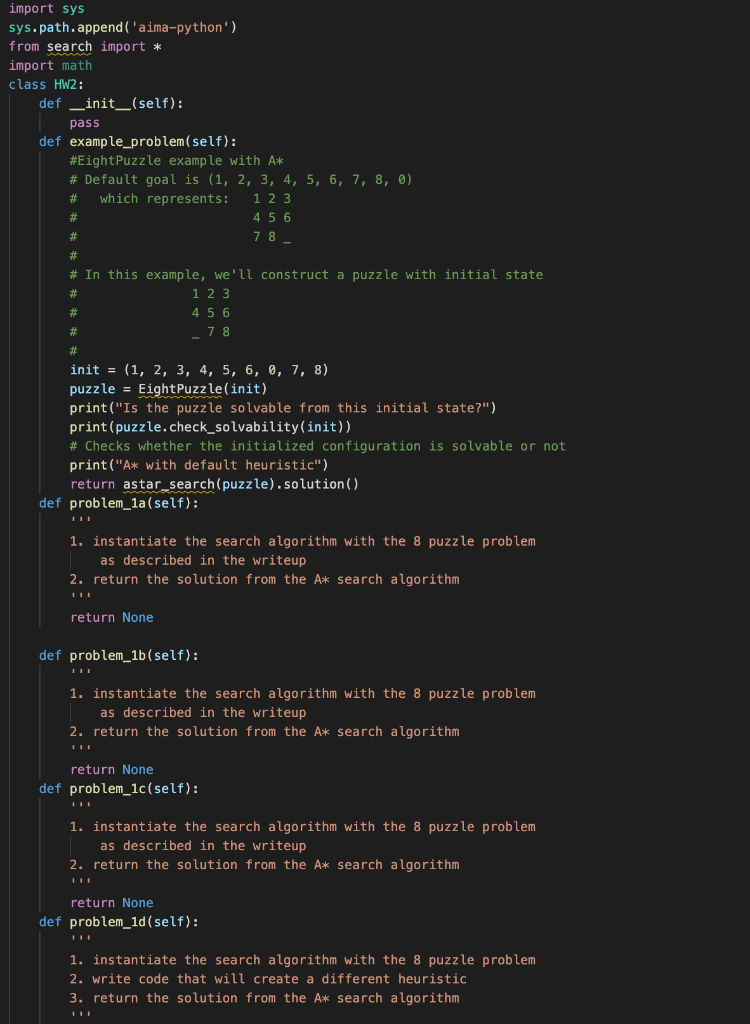
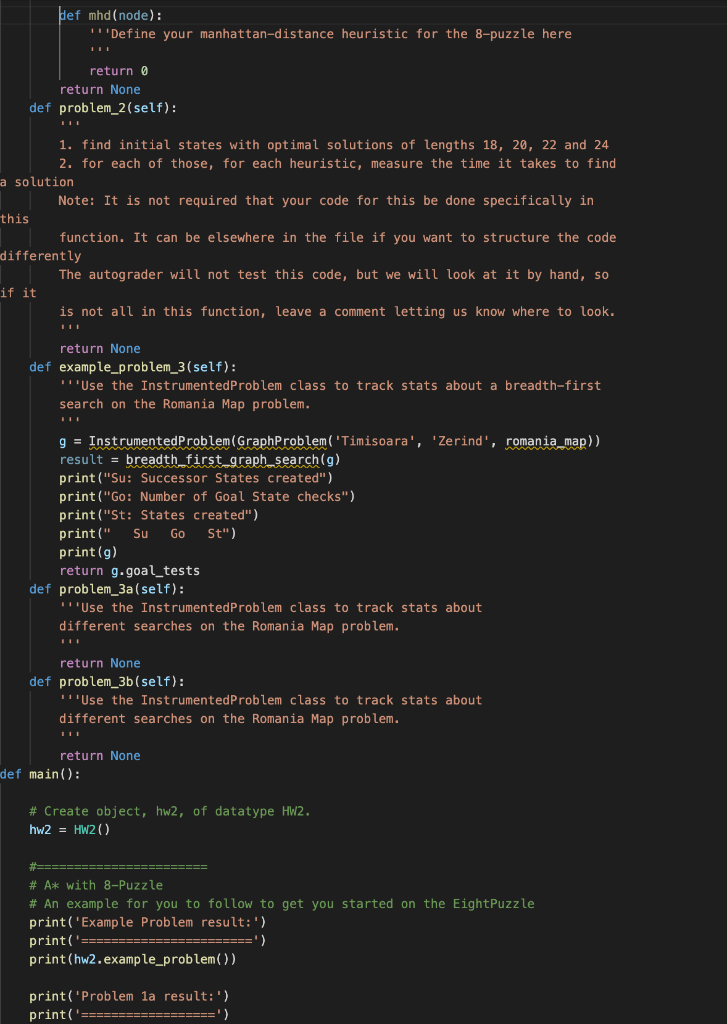
import sys sys.path.append('aima-python') from search import * import math class HW2: def __init__(self): pass def example_problem(self): #EightPuzzle example with A* # Default goal is (1, 2, 3, 4, 5, 6, 7, 8, 0) # which represents: 1 2 3 # 4 5 6 # 7 8 _ # # In this example, we'll construct a puzzle with initial state # 1 2 3 # 4 5 6 # _ 7 8 # init = (1, 2, 3, 4, 5, 6, 0, 7, 8) puzzle = EightPuzzle(init) print("Is the puzzle solvable from this initial state?") print(puzzle.check_solvability(init)) # Checks whether the initialized configuration is solvable or not print("A* with default heuristic") return astar_search(puzzle).solution() def problem_1a(self): ''' 1. instantiate the search algorithm with the 8 puzzle problem as described in the writeup 2. return the solution from the A* search algorithm ''' return None def problem_1b(self): ''' 1. instantiate the search algorithm with the 8 puzzle problem as described in the writeup 2. return the solution from the A* search algorithm ''' return None def problem_1c(self): ''' 1. instantiate the search algorithm with the 8 puzzle problem as described in the writeup 2. return the solution from the A* search algorithm ''' return None def problem_1d(self): ''' 1. instantiate the search algorithm with the 8 puzzle problem 2. write code that will create a different heuristic

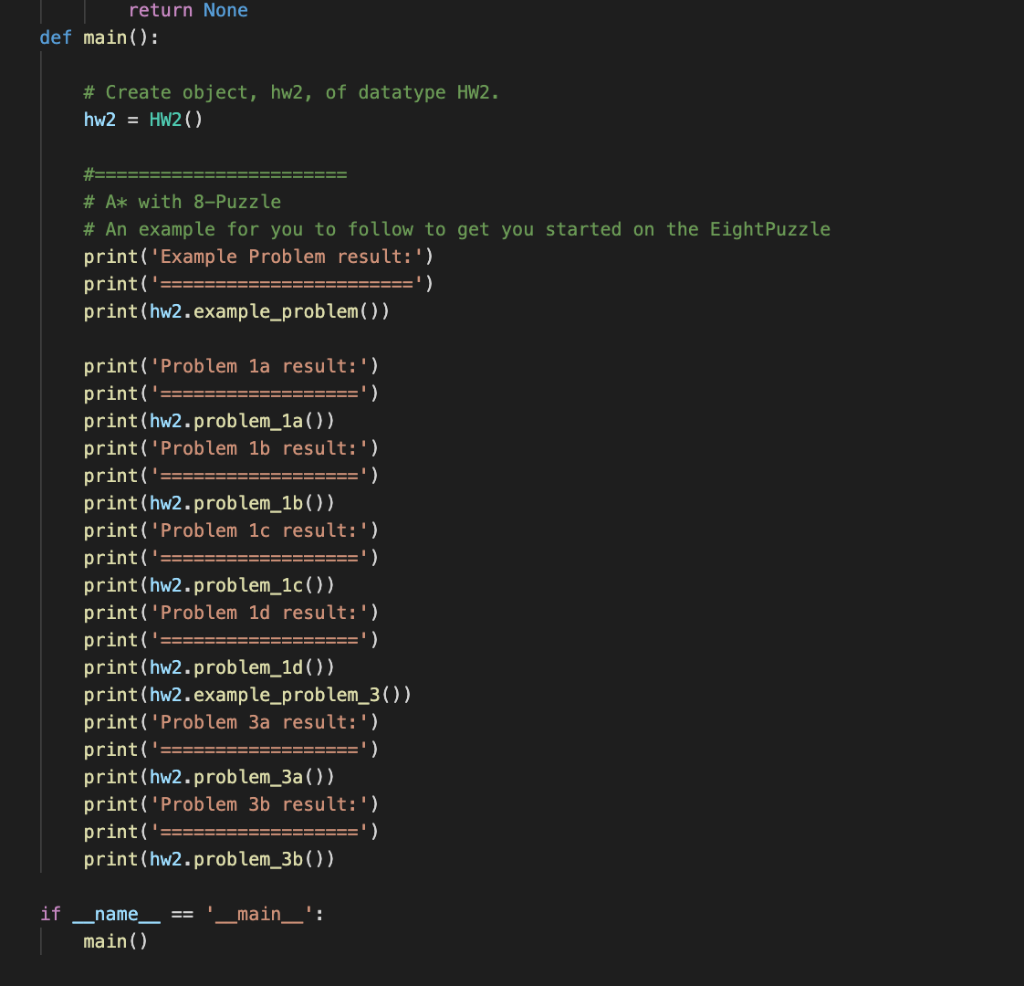
3. return the solution from the A* search algorithm ''' def mhd(node): '''Define your manhattan-distance heuristic for the 8-puzzle here ''' return 0 return None def problem_2(self): ''' 1. find initial states with optimal solutions of lengths 18, 20, 22 and 24 2. for each of those, for each heuristic, measure the time it takes to find a solution Note: It is not required that your code for this be done specifically in this function. It can be elsewhere in the file if you want to structure the code differently The autograder will not test this code, but we will look at it by hand, so if it is not all in this function, leave a comment letting us know where to look. ''' return None def example_problem_3(self): '''Use the InstrumentedProblem class to track stats about a breadth-first search on the Romania Map problem. ''' g = InstrumentedProblem(GraphProblem('Timisoara', 'Zerind', romania_map)) result = breadth_first_graph_search(g) print("Su: Successor States created") print("Go: Number of Goal State checks") print("St: States created") print(" Su Go St") print(g) return g.goal_tests def problem_3a(self): '''Use the InstrumentedProblem class to track stats about different searches on the Romania Map problem. ''' return None def problem_3b(self): '''Use the InstrumentedProblem class to track stats about different searches on the Romania Map problem. ''' return None def main(): # Create object, hw2, of datatype HW2. hw2 = HW2() #======================= # A* with 8-Puzzle # An example for you to follow to get you started on the EightPuzzle print('Example Problem result:')

print('=======================') print(hw2.example_problem()) print('Problem 1a result:') print('==================') print(hw2.problem_1a()) print('Problem 1b result:') print('==================') print(hw2.problem_1b()) print('Problem 1c result:') print('==================') print(hw2.problem_1c()) print('Problem 1d result:') print('==================') print(hw2.problem_1d()) print(hw2.example_problem_3()) print('Problem 3a result:') print('==================') print(hw2.problem_3a()) print('Problem 3b result:') print('==================') print(hw2.problem_3b()) if __name__ == '__main__': main()

1,3 are coding.

2,4 are written