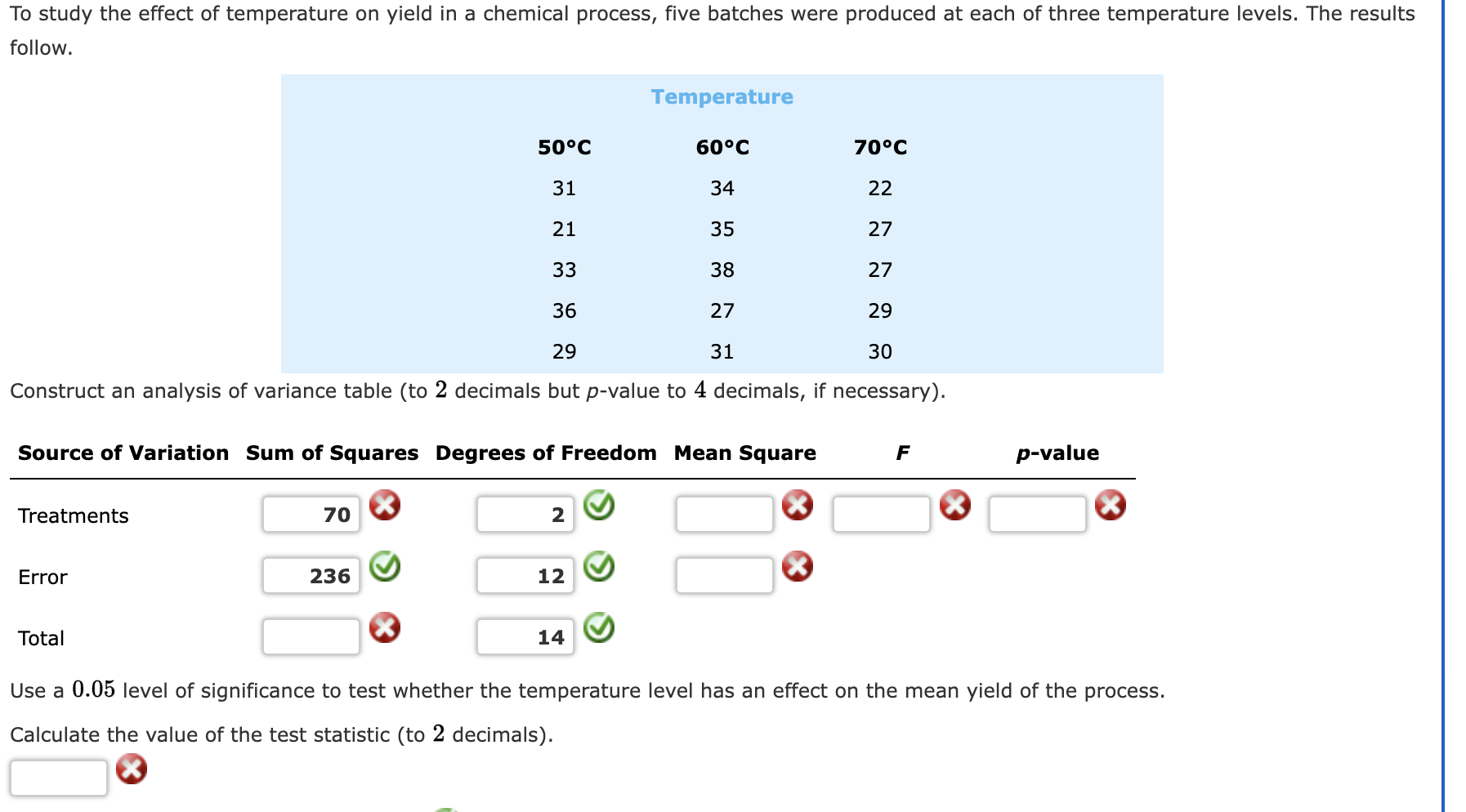
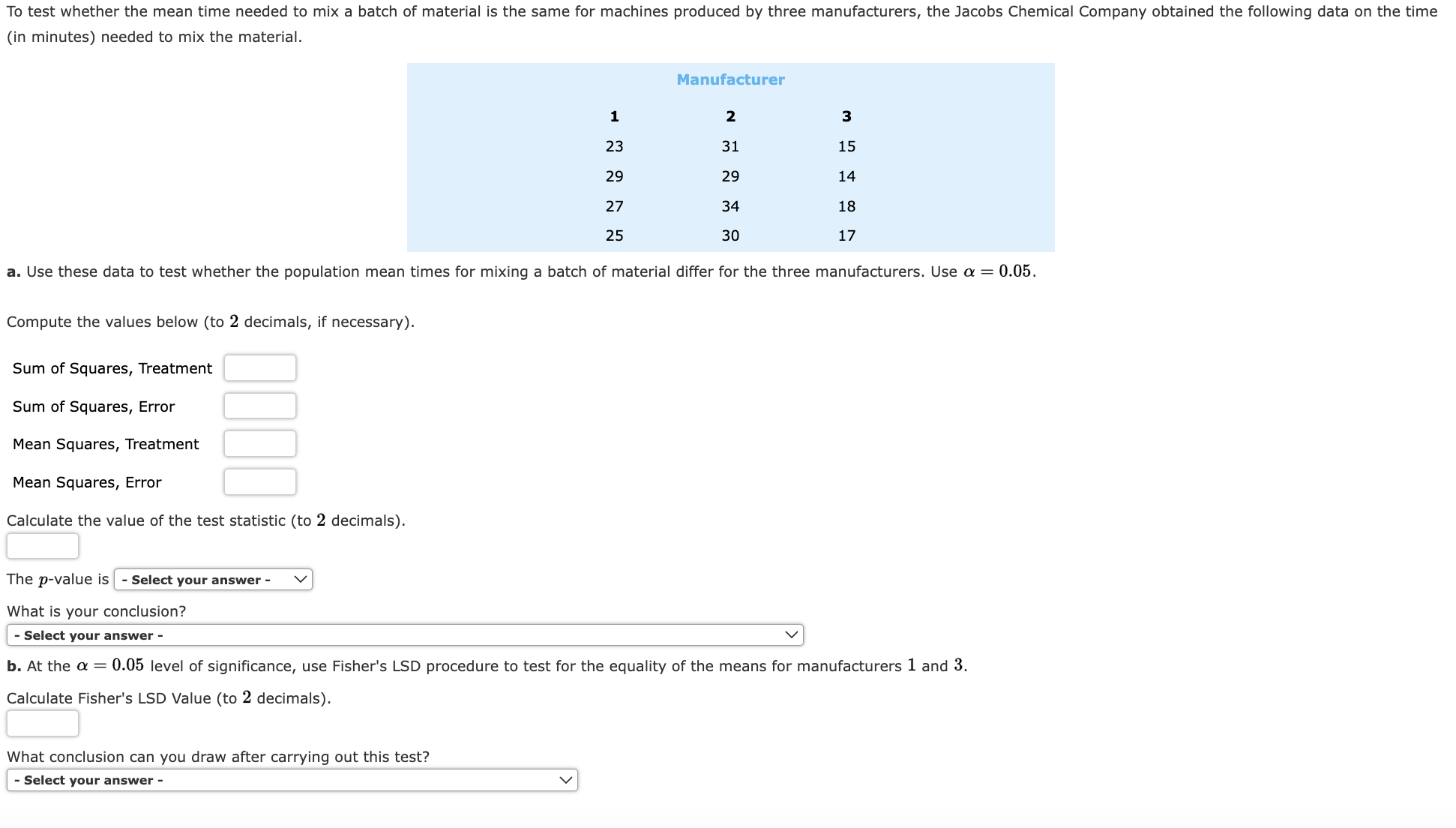
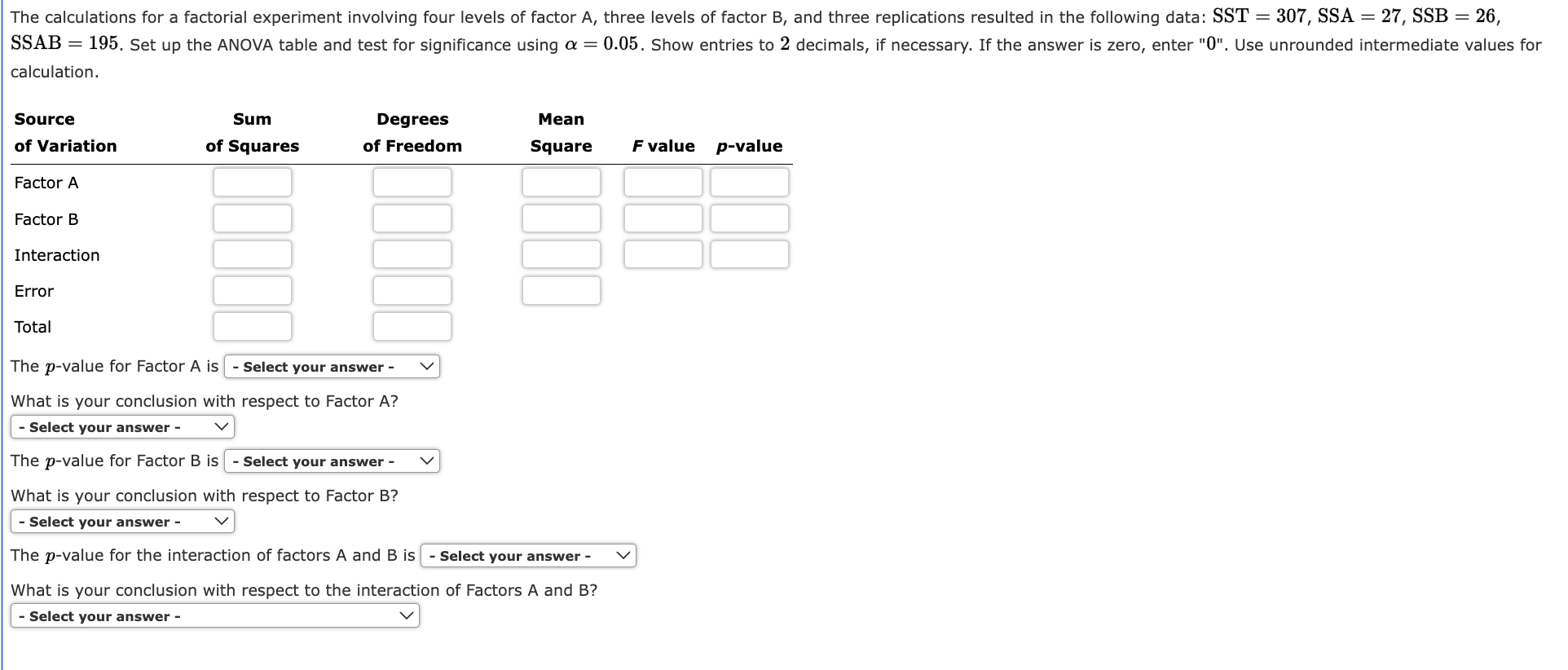
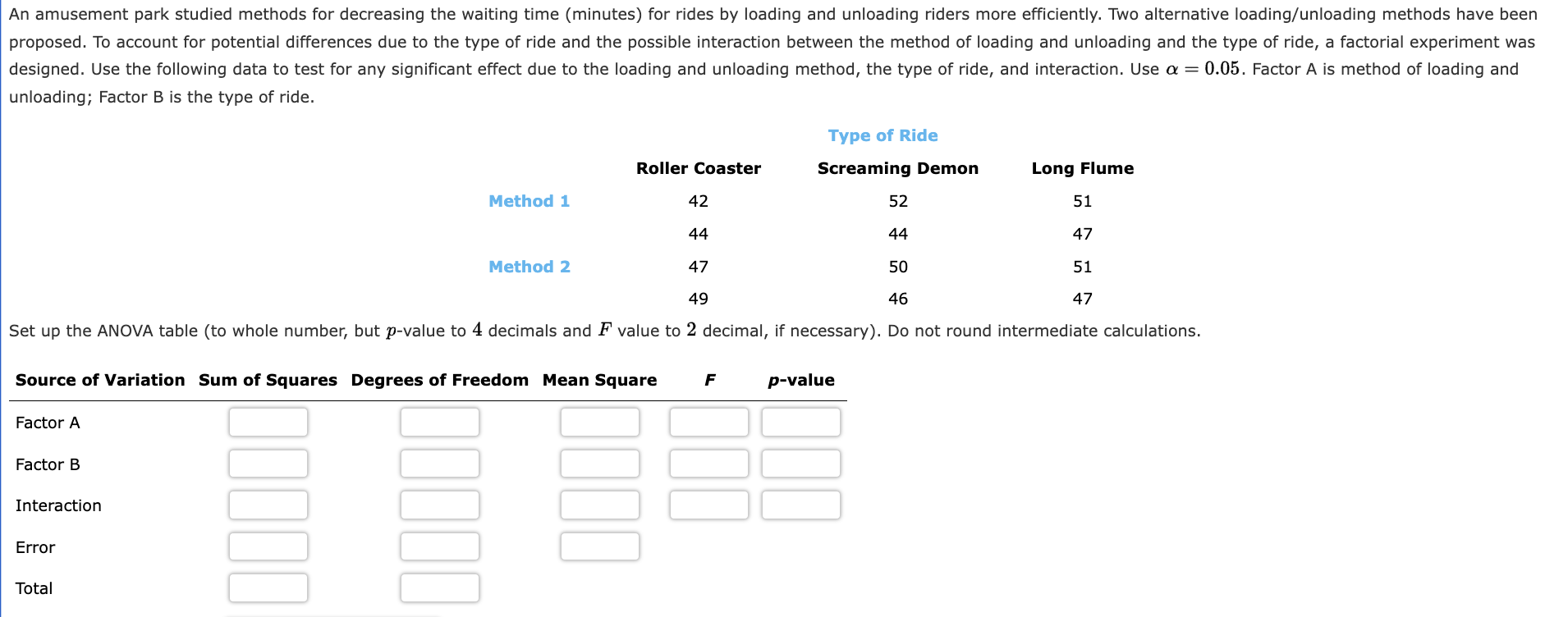
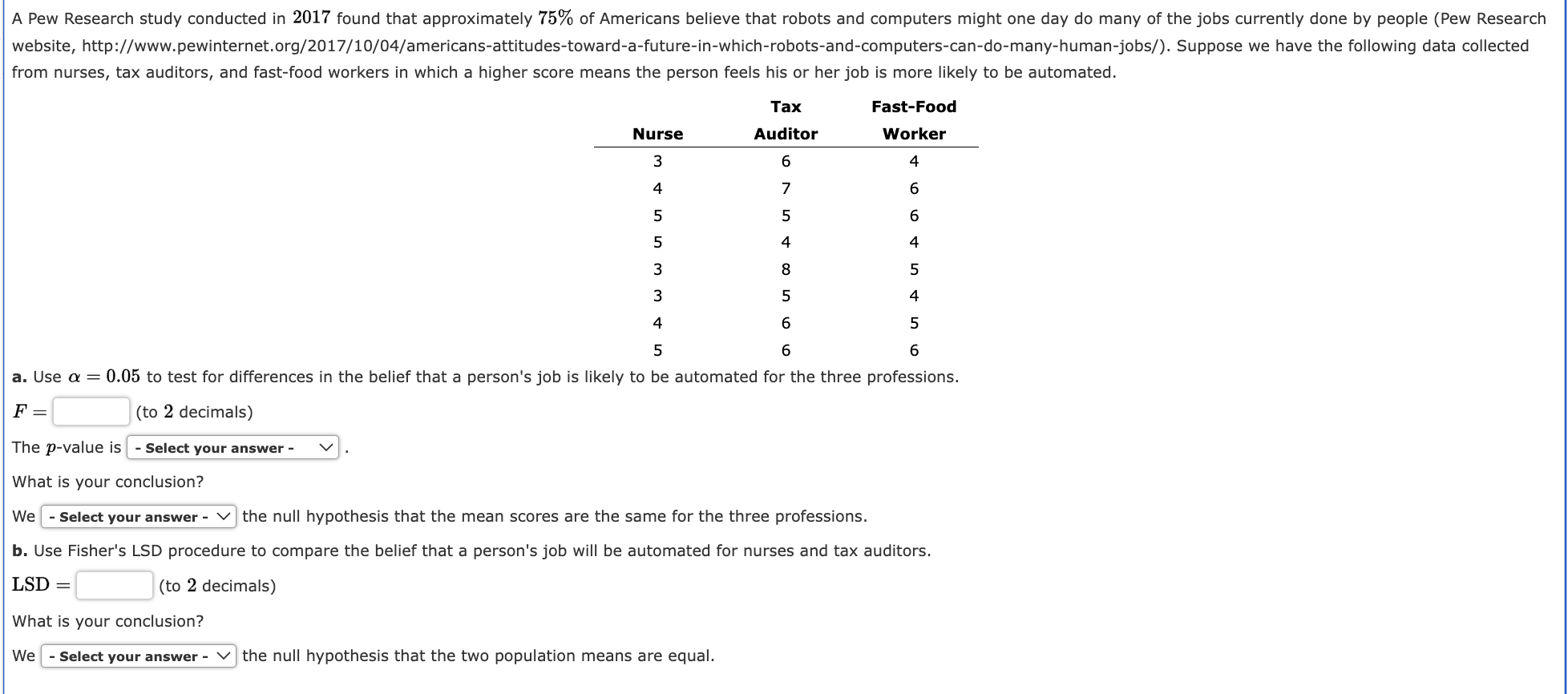
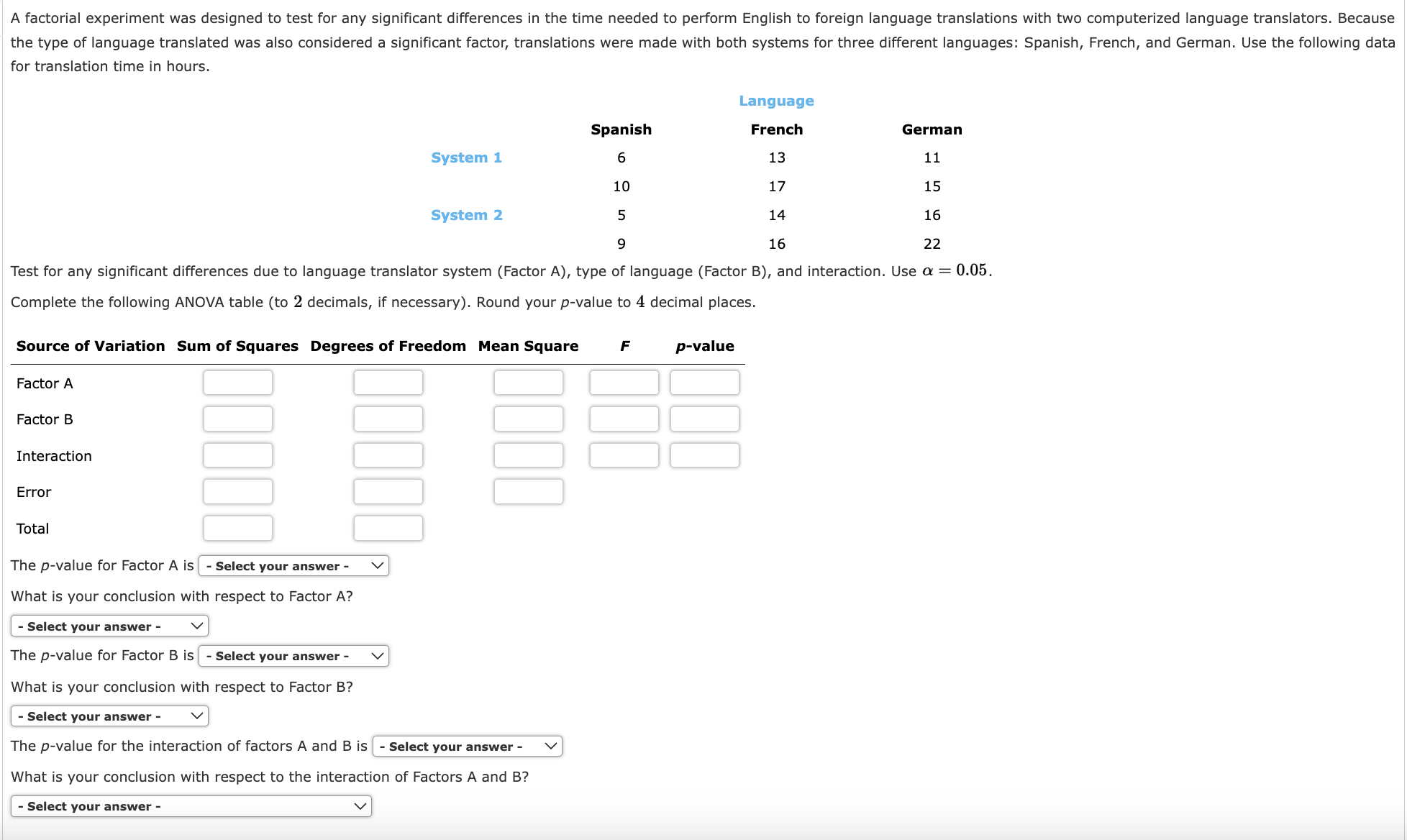
In a completely randomized design, 12 experimental units were used for the first treatment, 15 for the second treatment, and 20 for the third treatment. Complete the following analysis of variance (to 2 decimals, if necessary). If the answer is zero enter "0". Source of Variation Sum of Squares Degrees of Freedom Mean Square Treatments 1200 F p-value Error Total 1700 At a 0.05 level of significance, is there a significant difference between the treatments? The p-value is less than 0.01 What is your conclusion? Cannot conclude that the means of the three treatments are equal Three different methods for assembling a product were proposed by an industrial engineer. To investigate the number of units assembled correctly with each method, 30 employees were randomly selected and randomly assigned to the three proposed methods in such a way that each method was used by 10 workers. The number of units assembled correctly was recorded, and the analysis of variance procedure was applied to the resulting data set. The following results were obtained: SST =10,770; SSTR=4510. a. Set up the ANOVA table for this problem (to 2 decimals but p-value to 4 decimals, if necessary). Source of Variation Sum of Squares Degrees of Freedom Mean Square F p-value Treatments Error Total b.Use a = 0.05 to test for any significant difference in the means for the three assembly methods. Calculate the value of the test statistic (to 2 decimals). The p-value is less than 0.01 To study the effect of temperature on yield in a chemical process, five batches were produced at each of three temperature levels. The results follow. Temperature 50C 60C 70C 31 34 22 21 35 27 33 38 27 36 27 29 29 31 30 Construct an analysis of variance table (to 2 decimals but p-value to 4 decimals, if necessary). Source of Variation Sum of Squares Degrees of Freedom Mean Square F p-value Treatments Error Total 70 2 236 12 14 Use a 0.05 level of significance to test whether the temperature level has an effect on the mean yield of the process. Calculate the value of the test statistic (to 2 decimals). To test whether the mean time needed to mix a batch of material is the same for machines produced by three manufacturers, the Jacobs Chemical Company obtained the following data on the time (in minutes) needed to mix the material. Manufacturer 12222 2 3 23 31 15 29 29 14 27 25 34 18 30 17 a. Use these data to test whether the population mean times for mixing a batch of material differ for the three manufacturers. Use = 0.05. Compute the values below (to 2 decimals, if necessary). Sum of Squares, Treatment Sum of Squares, Error Mean Squares, Treatment Mean Squares, Error Calculate the value of the test statistic (to 2 decimals). The p-value is - Select your answer - What is your conclusion? - Select your answer - b. At the = 0.05 level of significance, use Fisher's LSD procedure to test for the equality of the means for manufacturers 1 and 3. Calculate Fisher's LSD Value (to 2 decimals). What conclusion can you draw after carrying out this test? - Select your answer - The calculations for a factorial experiment involving four levels of factor A, three levels of factor B, and three replications resulted in the following data: SST = 307, SSA = 27, SSB = 26, SSAB = 195. Set up the ANOVA table and test for significance using = 0.05. Show entries to 2 decimals, if necessary. If the answer is zero, enter "0". Use unrounded intermediate values for calculation. Source Sum Degrees Mean of Variation of Squares of Freedom Square F value p-value Factor A Factor B Interaction Error Total The p-value for Factor A is Select your answer - What is your conclusion with respect to Factor A? - Select your answer - The p-value for Factor B is - Select your answer - What is your conclusion with respect to Factor B? - Select your answer - The p-value for the interaction of factors A and B is Select your answer - What is your conclusion with respect to the interaction of Factors A and B? - Select your answer - An amusement park studied methods for decreasing the waiting time (minutes) for rides by loading and unloading riders more efficiently. Two alternative loading/unloading methods have been proposed. To account for potential differences due to the type of ride and the possible interaction between the method of loading and unloading and the type of ride, a factorial experiment was designed. Use the following data to test for any significant effect due to the loading and unloading method, the type of ride, and interaction. Use = 0.05. Factor A is method of loading and unloading; Factor B is the type of ride. 52 Roller Coaster Type of Ride Screaming Demon Long Flume Method 1 42 51 44 Method 2 49 44 50 46 47 51 47 EITT 47 Set up the ANOVA table (to whole number, but p-value to 4 decimals and F value to 2 decimal, if necessary). Do not round intermediate calculations. Source of Variation Sum of Squares Degrees of Freedom Mean Square F p-value Factor A Factor B Interaction Error Total A Pew Research study conducted in 2017 found that approximately 75% of Americans believe that robots and computers might one day do many of the jobs currently done by people (Pew Research website, http://www.pewinternet.org/2017/10/04/americans-attitudes-toward-a-future-in-which-robots-and-computers-can-do-many-human-jobs/). Suppose we have the following data collected from nurses, tax auditors, and fast-food workers in which a higher score means the person feels his or her job is more likely to be automated. Nurse 3 Tax Auditor Fast-Food Worker 6 4 4 7 6 5533 5 6 4 4 3 8 5 5 4 4 5 6 6 5 6 a. Use a = 0.05 to test for differences in the belief that a person's job is likely to be automated for the three professions. (to 2 decimals) F = The p-value is - Select your answer - What is your conclusion? We - Select your answer the null hypothesis that the mean scores are the same for the three professions. b. Use Fisher's LSD procedure to compare the belief that a person's job will be automated for nurses and tax auditors. LSD (to 2 decimals) What is your conclusion? We Select your answer - the null hypothesis that the two population means are equal. A factorial experiment was designed to test for any significant differences in the time needed to perform English to foreign language translations with two computerized language translators. Because the type of language translated was also considered a significant factor, translations were made with both systems for three different languages: Spanish, French, and German. Use the following data for translation time in hours. Spanish Language French German System 1 6 13 11 10 17 15 System 2 5 14 16 9 16 22 Test for any significant differences due to language translator system (Factor A), type of language (Factor B), and interaction. Use = 0.05. Complete the following ANOVA table (to 2 decimals, if necessary). Round your p-value to 4 decimal places. Source of Variation Sum of Squares Degrees of Freedom Mean Square F p-value Factor A Factor B Interaction Error Total 00000 The p-value for Factor A is Select your answer - What is your conclusion with respect to Factor A? - Select your answer - The p-value for Factor B is Select your answer - What is your conclusion with respect to Factor B? - Select your answer - The p-value for the interaction of factors A and B is - Select your answer - What is your conclusion with respect to the interaction of Factors A and B? - Select your answer -