In C++ Please

    
 

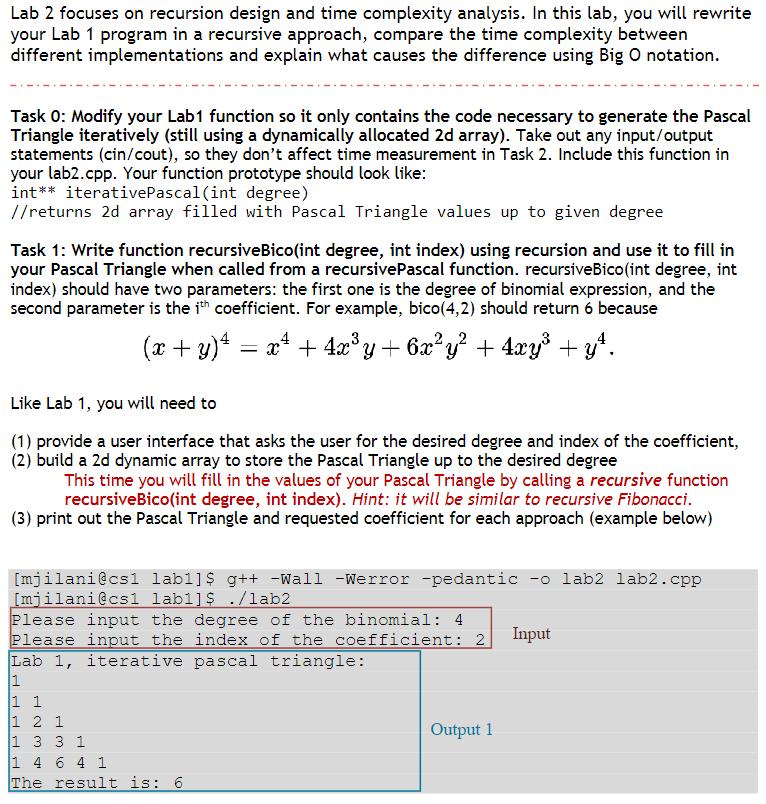
Lab 2 focuses on recursion design and time complexity analysis. In this lab, you will rewrite your Lab 1 program in a recursive approach, compare the time complexity between different implementations and explain what causes the difference using Big O notation. Task 0: Modify your Lab1 function so it only contains the code necessary to generate the Pascal Triangle iteratively (still using a dynamically allocated 2d array). Take out any input/output statements (cin/cout), so they don't affect time measurement in Task 2. Include this function in your lab2.cpp. Your function prototype should look like: int** iterative Pascal (int degree) //returns 2d array filled with Pascal Triangle values up to given degree Task 1: Write function recursiveBico(int degree, int index) using recursion and use it to fill in your Pascal Triangle when called from a recursive Pascal function. recursive Bico (int degree, int index) should have two parameters: the first one is the degree of binomial expression, and the second parameter is the ith coefficient. For example, bico (4,2) should return 6 because (x + y) = x + 4xy + 6xy + 4xy + y. Like Lab 1, you will need to (1) provide a user interface that asks the user for the desired degree and index of the coefficient, (2) build a 2d dynamic array to store the Pascal Triangle up to the desired degree This time you will fill in the values of your Pascal Triangle by calling a recursive function recursiveBico(int degree, int index). Hint: it will be similar to recursive Fibonacci. (3) print out the Pascal Triangle and requested coefficient for each approach (example below) [mjilani@cs1 labl] $ g++ -Wall -Werror -pedantic -o lab2 lab2.cpp [mjilani@cs1 labi] $ ./lab2 Please input the degree of the binomial: 4 Please input the index of the coefficient: 2 Input Lab 1, iterative pascal triangle: 1 1 1 2 1 1 3 3 1 1 4 6 4 1 The result is: 6 Output 1