In C++This program will utilize concepts of geometry and trigonometry. Write a program which determines how steep the climb is to the top of a mountain. The program will take user input which looks like the following:

1 2 3 2 2 2 

This represents a two-dimensional rectangle of integers. We are looking at a mountain (or mountains) from above (think of flying over a Minecraft landscape), and the area has a rectangular base. Each value is the height of the terrain at that specific point in the rectangle (in increments of 1 on both axes). Each horizontal row will be on a new line, and the end of the entire input will be noted with an empty line with no integers.

In this example, the top left corner is the lowest point with a height/elevation of 1 and the top right corner is the peak of the mountain at height 3.

The horizontal distance between each point is the standard 2-dimensional distance. In this example, the distance between the top left and top right corners is 2, and the distance between the top left and bottom right corners is sqrt(5) because of the Pythogrean Rule.

Your program should find lowest and highest heights in the input. It should then compute the angle between a line between the terrain at those two points and the horizontal plane (i.e. the angle you would be climbing if you went in a straight line from the lowest to highest point). The angle should then be printed in radians.

Using the example above, you can visualize the lowest and highest points (they happen to be on the same horizontal) and the angle made in the diagram below:

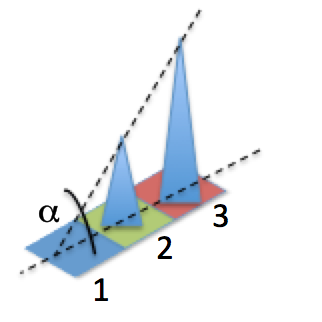
With the heights given above, the horizontal distance between the lowest and highest points is 2 and the change in height is also 2 (lowest at 1 to highest at 3). Therefore the angle of the line between them (from the horizontal) is 45 degrees or 0.785 radians.

Hint: remember that the distance between two points, (x₁, y₁) and (x₂, y₂), is the square root of ( (x₁ - x₂)² + (y₁ - y₂)² ).

Hint: the library contains the arctangent function, with the name atan().

Note: Assume that the lowest and the highest points are unique. This may not be true for other points.

REQUIRED: The input MUST be stored in a multidimensional integer array. The rectangle of heights will have a size less than or equal to 10 by 10. The program must utilize functions in the design. You are required to have at least one function that passes an array. You may not use any C++ functions that we have NOT discussed in lecture.

The program should print a string of text to the terminal before getting each line of input from the user. A session should look like one of the following examples (including whitespace and formatting), with a possibly numbers and letters in the output:

Enter heights: 5 5 6 5 5 6 7 6 5 5 6 6 3 4 4 5 2 3 3 3 2 2 2 2 1 2 2 2 The angle of the climb is 0.839 radians. 

or

Enter heights: 1 2 3 The angle of the climb is 0.785 radians. 

The string printed by the program should include a newline at the end, but no other trailing whitespace (whitespace at the end of the line).

The angle, in radians, should be printed to three places after the decimal.

This program will utilize concepts of geometry and trigonometry. Write a program which determines how steep the climb is to the top of a mountain. The program will take user input which looks like the following: 1 2 3 2 2 2 This represents a two-dimensional rectangle of integers. We are looking at a mountain (or mountains) from above (think of flying over a Minecraft landscape), and the area has a rectangular base. Each value is the height of the terrain at that specific point in the rectangle (in increments of 1 on both axes). Each horizontal row will be on a new line, and the end of the entire input will be noted with an empty line with no integers In this example, the top left corner is the lowest point with a height/elevation of 1 and the top right corner is the peak of the mountain at height 3 The horizontal distance between each point is the standard 2-dimensional distance. In this example, the distance between the top left and top right corners is 2, and the distance between the top left and bottom right corners is because of the Pythogrean Rule Your program should find lowest and highest heights in the input. It should then compute the angle between a line between the terrain at those two points and the horizontal plane (i.e. the angle you would be climbing if you went in a straight line from the lowest to highest point). The angle should then be printed in radians. Using the example above, you can visualize the lowest and highest points (they happen to be on the same horizontal) and the angle made in the diagram below: With the heights given above, the horizontal distance between the lowest and highest points is 2 and the change in height is also 2 (lowest at 1 to highest at 3). Therefore the angle of the line between them (from the horizontal) is 45 degrees or 0.785 radians Hint: remember that the distance between two points, (x1, y1) and (xa, y2), is the square root of (x1 X2 (y1-ya)2 Hint: the library contains the arctangent function, with the name atan0 Note: Assume that the lowest and the highest points are unique. This may not be true for other points