In capital-budgeting problems within the firm, there is a debate as to whether or not the appropriate objective function should be discounted. The formulation of the capital-budgeting problem without discounting is as follows:

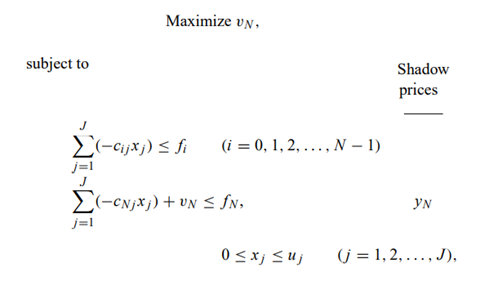
where ci j is the cash outflow (ci j i j > 0) in period i for project j; the righthand-side constant fi is the net exogenous funds made available to (fi > 0) or withdrawn from (fi j is the level of investment in project j; u j is an upper bound on the level of investment in project j; and vN is a variable measuring the value of the holdings of the division at the end of the planning horizon. If the undiscounted problem is solved by the bounded variable simplex method, the optimal solution is x ∗ j for j = 1, 2, . . . , J with associated shadow prices (dual variables) y ∗ i for i = 0, 1, 2, . . . , N.

 a) Show that y ∗ N = 1.

 b) The discount factor for time i is defined to be the present value (time i = 0) of one dollar received at time i. Show that the discount factor for time i, ρ ∗ i is given by:

(Assume that the initial budget constraint is binding so that y ∗ 0 > 0.)

c) Why should ρ ∗ 0 = 1?

Transcribed Image Text:

subject to Maximize UN, j=1 (-Cjxj) fi (i = 0, 1, 2, ..., N-1) (CNjXj)+UN SN, 0xj uj Shadow prices YN (j= 1,2,..., J), subject to Maximize UN, j=1 (-Cjxj) fi (i = 0, 1, 2, ..., N-1) (CNjXj)+UN SN, 0xj uj Shadow prices YN (j= 1,2,..., J),