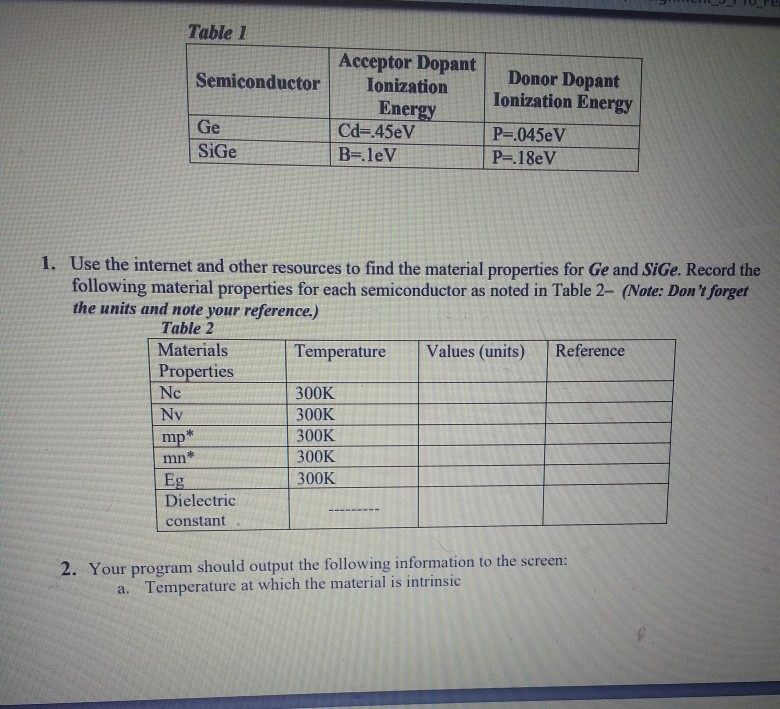
In class, we derived quantifatively how the electron and hole concentrations chango ns the Fermi energy level moves through the bandgap energy where, exp(& c) (4-4) and p N exp kT Assume Ec Eg and Ev DeV These expressions are based upon the probability that an available state is occupied or empty. In like manner, we can apply probability statistics to obtain expressions for the number of donor and acceptor energy states where, and N 1+2 expkT Ep -Ep EA is the acceptor ionization energy (ie. the amount of energy needed for an electron in the valence band to be excited to occupy the acceptor site) and Ep is the donor ionization energy (ie. the amount of energy needed for an electron be excited from the donor site to the conduction band). You will use the expressions noted above to determine the position of the Fermi energy level for various semiconductors as a function of acceptor and donor doping and temperature, similar to the plot noted in Lecture 14 Part I. With the help of a computer software program (C, Fortran, or Pascal) or a commercial software package such as Mathematica, Maple or Matlab use the charge neutrality equat in order to a) Plot the Fermi level relative to Ei (Ef-Ei) as a function of doping vs temperature In class, we derived quantifatively how the electron and hole concentrations chango ns the Fermi energy level moves through the bandgap energy where, exp(& c) (4-4) and p N exp kT Assume Ec Eg and Ev DeV These expressions are based upon the probability that an available state is occupied or empty. In like manner, we can apply probability statistics to obtain expressions for the number of donor and acceptor energy states where, and N 1+2 expkT Ep -Ep EA is the acceptor ionization energy (ie. the amount of energy needed for an electron in the valence band to be excited to occupy the acceptor site) and Ep is the donor ionization energy (ie. the amount of energy needed for an electron be excited from the donor site to the conduction band). You will use the expressions noted above to determine the position of the Fermi energy level for various semiconductors as a function of acceptor and donor doping and temperature, similar to the plot noted in Lecture 14 Part I. With the help of a computer software program (C, Fortran, or Pascal) or a commercial software package such as Mathematica, Maple or Matlab use the charge neutrality equat in order to a) Plot the Fermi level relative to Ei (Ef-Ei) as a function of doping vs temperature