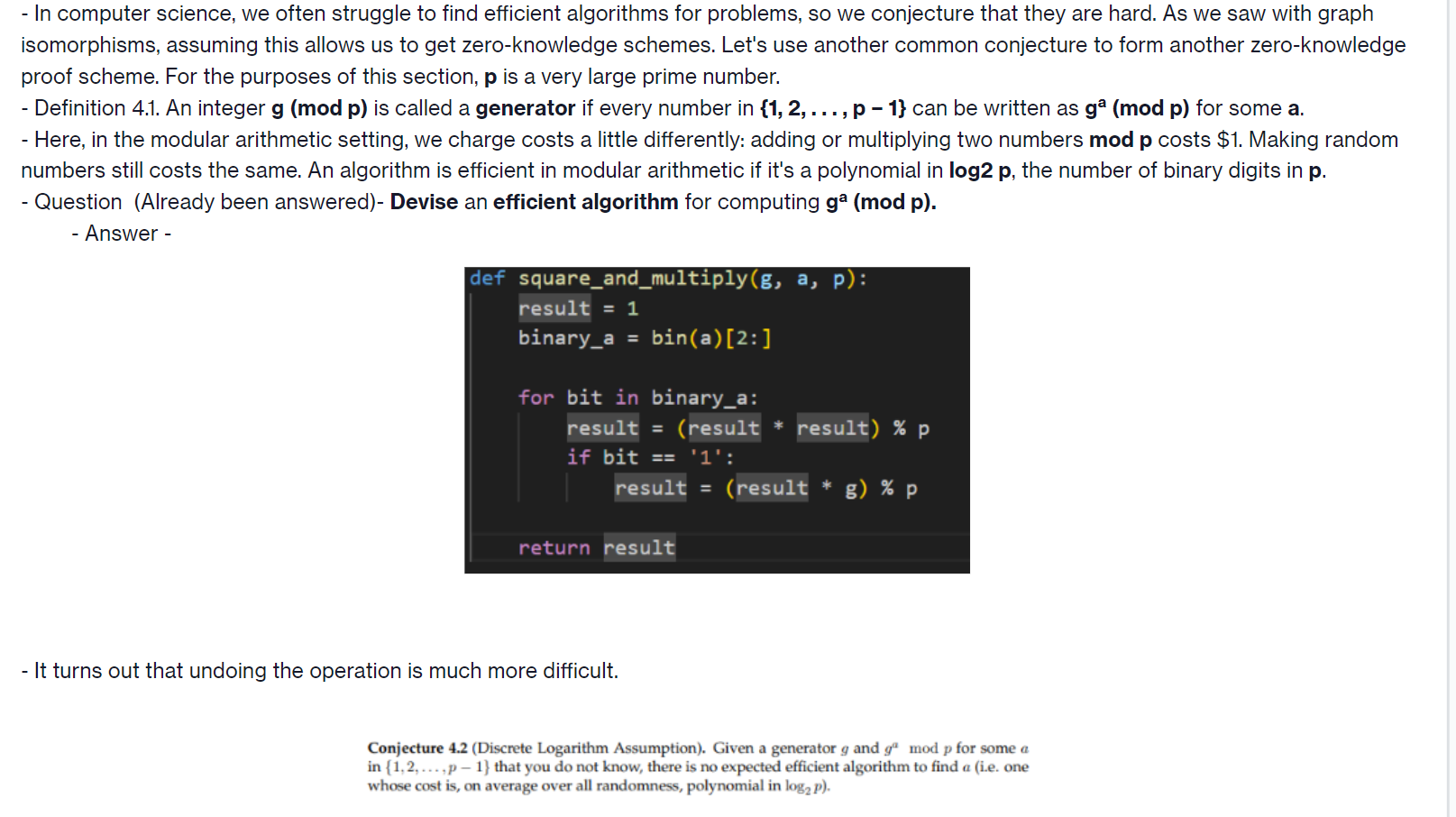
- In computer science, we often struggle to find efficient algorithms for problems, so we conjecture that they are hard. As we saw with graph isomorphisms, assuming this allows us to get zero-knowledge schemes. Let's use another common conjecture to form another zero-knowledge proof scheme. For the purposes of this section, p is a very large prime number. Definition 4.1. An integer g (mod p) is called a generator if every number in {1, 2, ..., p - 1} can be written as g (mod p) for some a. - Here, in the modular arithmetic setting, we charge costs a little differently: adding or multiplying two numbers mod p costs $1. Making random numbers still costs the same. An algorithm is efficient in modular arithmetic if it's a polynomial in log2 p, the number of binary digits in p. - Question (Already been answered)- Devise an efficient algorithm for computing ga (mod p). - Answer - - def square_and_multiply(g, a, p): result = 1 binary_a = bin(a) [2:] for bit in binary_a: result = (result * result) % p if bit == '1': result = (result * g) % p return result - It turns out that undoing the operation is much more difficult. Conjecture 4.2 (Discrete Logarithm Assumption). Given a generator g and g mod p for some a in {1,2,...,p-1)} that you do not know, there is no expected efficient algorithm to find a (i.e. one whose cost is, on average over all randomness, polynomial in log p). Suppose now that everyone has access to the same prime p and a generator g (mod p). Paula picks a random number a from the set {1,2,...,p- 1} and gives Victor u = g. Victor and Paula want to make a scheme so Victor can identify Paula in communications, without Victor himself being able to impersonate Paula. Question 4.4 (20 pts). Construct a ZKP scheme that allows Paula to convince Victor that she knows a, and does not allow others to convince Victor they know a. Here is a possible scheme with some steps removed that you can use as a template. 1. When she wants to log in, Paula chooses randomly at & Zp (where Zp is the set {0, 1, 2, ..., p- 1}), computes ut = mod p and sends ut to Victor. 2. Victor chooses randomly c Zp and sends c to Paula. 3. Paula computes az = mod p and sends it to Victor. (mod p). 4. Victor accepts the proof if gaz = Discuss the soundness and completeness of your scheme, and provide an efficient simulator for the transcript.