In JAVA, please code the following program:

AVL Versus Simple Binary Search Trees

I've provided the following java files that are needed for this program: ForestAnalyzer.java , AVLTree.java , AVLTreeAPI.java , BSTree.java , BSTreeAPI.java, only the methods that say "//implement this method" should be modified and implemented. Below the java code files, I've provided the sample command text file: smalltrees.ops, as well as the sample output file: smalltrees.out . Use these to test the code.

ForestAnalyzer.java

package forestanalyzer; import java.io.FileReader; import java.io.IOException; import java.io.PrintStream; import java.util.Scanner; import java.util.function.Function;

/** * Performs insertions and searches, using the same data set,on a binary search * tree and an AVL tree to compare the performance of * these operations on the trees. */ public class ForestAnalyzer { /** * @param args the command line arguments * @throws AVLTreeException * @throws BSTreeException * @throws java.io.IOException */ public static void main(String[] args) throws AVLTreeException, BSTreeException, IOException { //Implement this method } }

AVLTree.java

package forestanalyzer; import java.util.ArrayList; import java.util.concurrent.atomic.AtomicBoolean; import java.util.function.Function;

/** * Models an AVL tree. * @param data type of elements of the tree * @see AVLTreeAPI, AVLTreeException */

public class AVLTree> implements AVLTreeAPI { /** * The root node of this tree */ private Node root; /** * The number of nodes in this tree */ private int count; /** * A node of a tree stores a data item and references * to the child nodes to the left and to the right. */ private class Node { /** * the data in this node */ public E data; /** * the left child */ public Node left; /** * the right child */ public Node right; /** * the balanced factor of this node */ BalancedFactor bal; } /** Constructs an empty tree */ public AVLTree() { root = null; count = 0; }

public boolean isEmpty() { return (root == null); }

public void insert(E obj) { Node newNode = new Node(); newNode.bal = BalancedFactor.EH; newNode.data = obj; AtomicBoolean forTaller = new AtomicBoolean(); if (!inTree(obj)) count++; root = insert(root,newNode, forTaller);

}

public boolean inTree(E item) { Node tmp; if (isEmpty()) return false; /*find where it is */ tmp = root; while (true) { int d = tmp.data.compareTo(item); if (d == 0) return true; else if (d > 0) { if (tmp.left == null) return false; else /* continue searching */ tmp = tmp.left; } else { if (tmp.right == null) return false; else /* continue searching for insertion pt. */ tmp = tmp.right; } } }

public void remove(E item) { AtomicBoolean shorter = new AtomicBoolean(); AtomicBoolean success = new AtomicBoolean(); Node newRoot; if (!inTree(item)) return; newRoot = remove(root,item, shorter, success); if (success.get()) { root = newRoot; count--; } }

public E retrieve(E item) throws AVLTreeException { Node tmp; if (isEmpty()) throw new AVLTreeException("AVL Tree Exception: tree empty on call to retrieve()"); /*find where it is */ tmp = root; while (true) { int d = tmp.data.compareTo(item); if (d == 0) return tmp.data; else if (d > 0) { if (tmp.left == null) throw new AVLTreeException("AVL Tree Exception: key not in tree call to retrieve()"); else /* continue searching */ tmp = tmp.left; } else { if (tmp.right == null) throw new AVLTreeException("AVL Tree Exception: key not in tree call to retrieve()"); else /* continue searching for insertion pt. */ tmp = tmp.right; } } }

public void traverse(Function func) { traverse(root,func); }

public int size() { return count; } /*===> BEGIN: Augmented public methods END: Augmented public methods

/** * A enumerated type for the balanced factor of a node */ private enum BalancedFactor { LH(-1),EH(0),RH(1); BalancedFactor(int aValue) { value = aValue; } private int value; }

/* private methods definitions */ /** * An auxiliary method that inserts a new node in the tree or * updates a node if the data is already in the tree. * @param curRoot a root of a subtree * @param newNode the new node to be inserted * @param taller indicates whether the subtree becomes * taller after the insertion * @return a reference to the new node */ private Node insert(Node curRoot, Node newNode, AtomicBoolean taller) { if (curRoot == null) { curRoot = newNode; taller.set(true); return curRoot; } int d = newNode.data.compareTo(curRoot.data); if (d 0) { curRoot.right = insert(curRoot.right,newNode,taller); if (taller.get()) switch(curRoot.bal) { case LH: // was left-high -- now EH curRoot.bal = BalancedFactor.EH; taller.set(false); break; case EH: // was balance -- now RH curRoot.bal = BalancedFactor.RH; break; case RH: //was right high -- rotate curRoot = rightBalance(curRoot,taller); break; } return curRoot; } else { curRoot.data = newNode.data; taller.set(false); return curRoot; } }

/** * An auxiliary method that left-balances the specified node * @param curRoot the node to be left-balanced * @param taller indicates whether the tree becomes taller * @return the root of the subtree after left-balancing */ private Node leftBalance(Node curRoot, AtomicBoolean taller) { Node rightTree; Node leftTree; leftTree = curRoot.left; switch(leftTree.bal) { case LH: //left-high -- rotate right curRoot.bal = BalancedFactor.EH; leftTree.bal = BalancedFactor.EH; // Rotate right curRoot = rotateRight(curRoot); taller.set(false); break; case EH: // This is an error System.out.println("AVL Tree Error: error in balance tree in call to leftBalance()"); System.exit(1); break; case RH: // right-high - requires double rotation: first left, then right rightTree = leftTree.right; switch(rightTree.bal) { case LH: curRoot.bal = BalancedFactor.RH; leftTree.bal = BalancedFactor.EH; break; case EH: curRoot.bal = BalancedFactor.EH; leftTree.bal = BalancedFactor.EH; /* LH */ break; case RH: curRoot.bal = BalancedFactor.EH; leftTree.bal = BalancedFactor.LH; break; } rightTree.bal = BalancedFactor.EH; // rotate left curRoot.left = rotateLeft(leftTree); //rotate right curRoot = rotateRight(curRoot); taller.set(false); } return curRoot; }

/** * An auxiliary method that right-balances the specified node * @param curRoot the node to be right-balanced * @param taller indicates whether the tree becomes taller * @return the root of the subtree after right-balancing */ private Node rightBalance(Node curRoot, AtomicBoolean taller) { Node rightTree; Node leftTree; rightTree = curRoot.right; switch(rightTree.bal) { case RH: //right-high -- rotate left curRoot.bal = BalancedFactor.EH; rightTree.bal = BalancedFactor.EH; // Rotate left curRoot = rotateLeft(curRoot); taller.set(false); break; case EH: // This is an error System.out.println("AVL Tree Error: error in balance tree in call to rightBalance()"); break; case LH: // left-high - requires double rotation: first right, then left leftTree = rightTree.left; switch(leftTree.bal) { case RH: curRoot.bal = BalancedFactor.LH; rightTree.bal = BalancedFactor.EH; break; case EH: curRoot.bal = BalancedFactor.EH; rightTree.bal = BalancedFactor.EH; /* RH */ break; case LH: curRoot.bal = BalancedFactor.EH; rightTree.bal = BalancedFactor.RH; break; } leftTree.bal = BalancedFactor.EH; // rotate right curRoot.right = rotateRight(rightTree); //rotate left curRoot = rotateLeft(curRoot); taller.set(false); } return curRoot; }

/** * An auxiliary method that Left-rotates the subtree at this node * @param node the node at which the left-rotation occurs. * @return the new node of the subtree after the left-rotation */ private Node rotateLeft(Node node) { Node tmp; tmp = node.right; node.right = tmp.left; tmp.left = node; return tmp; }

/** * An auxiliary method that right-rotates the subtree at this node * @param node the node at which the right-rotation occurs. * @return the new node of the subtree after the right-rotation */ private Node rotateRight(Node node) { Node tmp; tmp = node.left; node.left = tmp.right; tmp.right = node; return tmp; }

/** * An auxiliary method that in-order traverses the subtree at the specified node * @param node the root of a subtree * @param func the function to be applied to the data in each node */ private void traverse(Node node, Function func) { if (node != null) { traverse(node.left,func); func.apply(node.data); traverse(node.right,func); } }

/** * An auxiliary method that deletes the specified node from this tree * @param node the node to be deleted * @param key the item stored in this node * @param shorter indicates whether the subtree becomes shorter * @param success indicates whether the node was successfully deleted * @return a reference to the deleted node */ private Node remove(Node node, E key, AtomicBoolean shorter, AtomicBoolean success) { Node delPtr; Node exchPtr; Node newRoot; if (node == null) { shorter.set(false); success.set(false); return null; } int d = key.compareTo(node.data); if (d 0) { node.right = remove(node.right,key,shorter,success); if (shorter.get()) node = deleteLeftBalance(node,shorter); } else { delPtr = node; if (node.right == null) { newRoot = node.left; success.set(true); shorter.set(true); return newRoot; } else if(node.left == null) { newRoot = node.right; success.set(true); shorter.set(true); return newRoot; } else { exchPtr = node.left; while(exchPtr.right != null) exchPtr = exchPtr.right; node.data = exchPtr.data; node.left = remove(node.left,exchPtr.data,shorter,success); if (shorter.get()) node = deleteRightBalance(node,shorter); } } return node; } /** * An auxiliary method that right-balances this subtree after a deletion * @param node the node to be right-balanced * @param shorter indicates whether the subtree becomes shorter * @return a reference to the root of the subtree after right-balancing. */ private Node deleteRightBalance(Node node, AtomicBoolean shorter) { Node rightTree; Node leftTree; switch(node.bal) { case LH: //deleted left -- now balanced node.bal = BalancedFactor.EH; break; case EH: /ow right high node.bal = BalancedFactor.RH; shorter.set(false); break; case RH: // right high -- rotate left rightTree = node.right; if (rightTree.bal == BalancedFactor.LH) { leftTree = rightTree.left; switch(leftTree.bal) { case LH: rightTree.bal = BalancedFactor.RH; node.bal = BalancedFactor.EH; break; case EH: node.bal = BalancedFactor.EH; rightTree.bal = BalancedFactor.EH; break; case RH: node.bal = BalancedFactor.LH; rightTree.bal = BalancedFactor.EH; break; } leftTree.bal = BalancedFactor.EH; //rotate right, then left node.right = rotateRight(rightTree); node = rotateLeft(node); } else { switch(rightTree.bal) { case LH: case RH: node.bal = BalancedFactor.EH; rightTree.bal = BalancedFactor.EH; break; case EH: node.bal = BalancedFactor.RH; rightTree.bal = BalancedFactor.LH; shorter.set(false); break; } node = rotateLeft(node); } } return node; }

/** * An auxiliary method that left-balances this subtree after a deletion * @param node the node to be left-balanced * @param shorter indicates whether the subtree becomes shorter * @return a reference to the root of the subtree after left-balancing. */ private Node deleteLeftBalance(Node node, AtomicBoolean shorter) { Node rightTree; Node leftTree; switch(node.bal) { case RH: //deleted right -- now balanced node.bal = BalancedFactor.EH; break; case EH: /ow left high node.bal = BalancedFactor.LH; shorter.set(false); break; case LH: // left high -- rotate right leftTree = node.left; if (leftTree.bal == BalancedFactor.RH) { rightTree = leftTree.right; switch(rightTree.bal) { case RH: leftTree.bal = BalancedFactor.LH; node.bal = BalancedFactor.EH; break; case EH: node.bal = BalancedFactor.EH; leftTree.bal = BalancedFactor.EH; break; case LH: node.bal = BalancedFactor.RH; leftTree.bal = BalancedFactor.EH; break; } rightTree.bal = BalancedFactor.EH; //rotate left, then right node.left = rotateLeft(leftTree); node = rotateRight(node); } else { switch(leftTree.bal) { case RH: case LH: node.bal = BalancedFactor.EH; leftTree.bal = BalancedFactor.EH; break; case EH: node.bal = BalancedFactor.LH; leftTree.bal = BalancedFactor.RH; shorter.set(false); break; } node = rotateRight(node); } } return node; } /* BEGIN: Augmented Private Auxiliary Methods */ /** * Recursively computes the height of the subtree * rooted at the specified node * @param node the root of a subtree * @return the height of the subtree rooted at the * specified node */ private int height(Node node) { //Implement this method } /** * Recursively determines the diameter, the number of nodes on * the longest path, of the subtree rooted at the specified node * @param node the root of the specified subtree * @return the diameter of the tree rooted at the specified node */ private int diameter(Node node) { //Implement this method } /** * Recursively determines whether the subtree rooted at the * specified node is perfect. * @param node the root of a subtree * @param index the zero-based level-order index of this node * @return true if the tree root at the specified node is perfect; * otherwise, false */ private boolean isPerfect(Node node, int index) { //Implement this method } /** * Recursively determines whether the subtree rooted at the specified node * is full * @param node the root of a subtree of this tree * @return true if the subtree rooted at the specified node is full; otherwise, false */ private boolean isFull(Node node) { //Implement this method } /* END: Augmented Private Auxiliary Methods */ }

AVLTreeAPI.java

package forestanalyzer; import java.util.function.Function;

/** * Reports an exception in an AVL Tree */ class AVLTreeException extends Exception {

/** * Creates a new instance of AVLTreeException without detail * message. */ public AVLTreeException() { }

/** * Constructs an instance of AVLTreeException with the * specified detail message. * @param msg the detail message. */ public AVLTreeException(String msg) { super(msg); } }

/** * Describes operations on an AVLTree * @param the data type * @see AVLTreeException */ public interface AVLTreeAPI> { /** * Determines whether the tree is empty. * @return true if the tree is empty; otherwise, false */ boolean isEmpty();

/** * Inserts an item into the tree. * @param obj the value to be inserted. */ void insert(E obj);

/** * Determine whether an item is in the tree. * @param item item with a specified search key. * @return true on success; false on failure. */ boolean inTree(E item);

/** * Delete an item from the tree. * @param item item with a specified search key. */ void remove(E item);

/** * returns the item with the given search key. * @param key the key of the item to be retrieved * @return the item with the specified key * @throws AVLTreeException when no such element exists */ E retrieve(E key) throws AVLTreeException;

/** * This function traverses the tree in in-order * and calls the function Visit once for each node. * @param func the function to apply to the data in each node */ void traverse(Function func); /** * Returns the number of items stored in the tree. * @return the size of the tree. */ int size(); }

BSTree.java

package forestanalyzer; import java.util.ArrayList; import java.util.function.Function;

/** * A binary search tree * Requires JDK 1.8 for Function* * @param the tree data type * @since 99-99-9999 * @see BSTreeAPI, BSTreeException */ public class BSTree> implements BSTreeAPI { /** * the root of this tree */ private Node root; /** * the number of nodes in this tree */ private int count; /** * A node of a tree stores a data item and references * to the child nodes to the left and to the right. */ private class Node { /** * the data in this node */ public E data; /** * A reference to the left subtree rooted at this node. */ public Node left; /** * A reference to the right subtree rooted at this node */ public Node right; } /** * Constructs an empty tree */ public BSTree() { root = null; count = 0; }

public boolean isEmpty() { return count == 0; }

public void insert(E item) { Node newNode = new Node(); newNode.data = item; if (count == 0) { root = newNode; count++; } else { Node tmp = root; while (true) { int d = tmp.data.compareTo(item); if (d==0) { /* Key already exists. (update) */ tmp.data = item; return; } else if (d>0) { if (tmp.left == null) { /* If the key is less than tmp */ tmp.left = newNode; count++; return; } else { /* continue searching for insertion pt. */ tmp = tmp.left; } } else { if (tmp.right == null) {/* If the key is greater than tmp */ tmp.right = newNode; count++; return; } else { /* continue searching for insertion point*/ tmp = tmp.right; } } } } }

public boolean inTree(E item) { return search(item) != null; }

public void remove(E item) { Node nodeptr = search(item); if (nodeptr != null) { remove(nodeptr); count--; } }

public E retrieve(E key) throws BSTreeException { if (count == 0) throw new BSTreeException("Non-empty tree expected on retrieve()."); Node nodeptr = search(key); if (nodeptr == null) throw new BSTreeException("Existent key expected on retrieve()."); return nodeptr.data; }

public void traverse(Function func) { traverse(root,func); }

public int size() { return count; } /*===> BEGIN: Augmented public Methods

/** * Give the heigh of this tree. * @return the height of this tree */ public int height() { return height(root); } /** * Computes the diameter, the number of nodes on the longest * path, in this tree * @return the diameter of this tree */ public int diameter() { return diameter(root); }

/** * Determines whether or not this AVL tree is perfect. * @return true if this tree is perfect; otherwise, false */ public boolean isPerfect() { //Implement this Method } /** * Determines whether or not this tree is full * @return true if this tree is full; otherwise, false */ public boolean isFull() { return isFull(root); } /* END: Augmented public Methods */ /** * A recursive auxiliary method for the inorderTraver method that * @param node a reference to a Node object * @param func a function that is applied to the data in each * node as the tree is traversed in order. */ private void traverse(Node node, Function func) { if (node != null) { traverse(node.left,func); func.apply(node.data); traverse(node.right,func); } }

/** * An auxiliary method that supports the search method * @param key a data key * @return a reference to the Node object whose data has the specified key. */ private Node search(E key) { Node current = root; while (current != null) { int d = current.data.compareTo(key); if (d == 0) return current; else if (d > 0) current = current.left; else current = current.right; } return null; }

/** * An auxiliary method that gives a Node reference to the parent node of * the specified node * @param node a reference to a Node object * @return a reference to the parent node of the specified node */ private Node findParent(Node node) { Node tmp = root; if (tmp == node) return null; while(true) { assert tmp.data.compareTo(node.data) != 0; if (tmp.data.compareTo(node.data)>0) { /* this assert is not needed but just in case there is a bug */ assert tmp.left != null; if (tmp.left == node) return tmp; else tmp = tmp.left; } else { assert tmp.right != null; if (tmp.right == node) return tmp; else tmp = tmp.right; } } }

/** * An auxiliary method that deletes the specified node from this tree * @param node the node to be deleted */ private void remove(Node node) { E theData; Node parent, replacement; parent = findParent(node); if (node.left != null) { if (node.right != null) { replacement = node.right; while (replacement.left != null) replacement = replacement.left; theData = replacement.data; remove(replacement); node.data = theData; return; } else { replacement = node.left; } } else { if (node.right != null) replacement = node.right; else replacement = null; } if (parent==null) root = replacement; else if (parent.left == node) parent.left = replacement; else parent.right = replacement; } /* BEGIN: Augmented Private Auxiliary Methods */ /** * An auxiliary method that recursively determines the height * of a subtree rooted at the specified node. * @param node a root of a subtree. */ private int height(Node node) { //Implement this method } /** * Recursively determines the diameter, the number of nodes on * the longest path, of the subtree rooted at the specified node * @param node the root of the specified subtree * @return the diameter of the tree rooted at the specified node */ private int diameter(Node node) { //Implement this method } /** * Recursively determines whether the subtree rooted at the * specified node is perfect. * @param node the root of a subtree * @param index the zero-based level-order index of this node * @return true if the tree root at the specified node is perfect; * otherwise, false */ private boolean isPerfect(Node node, int index) { //Implement this method } /** * Recursively determines whether the subtree rooted at the specified node * is full * @param node the root of a subtree of this tree * @return true if the subtree rooted at the specified node is full; otherwise, false */ private boolean isFull(Node node) { //Implement this method } /* END: Augmented Private Auxiliary Methods */ }

BSTreeAPI.java

package forestanalyzer; import java.util.function.Function;

/** /** * Reports an exception in a binary search tree */ class BSTreeException extends Exception { /** * Creates a new instance of BSTreeException without detail * message. */ public BSTreeException() { }

/** * Constructs an instance of BSTreeException with the specified * detail message. * @param msg the detail message. */ public BSTreeException(String msg) { super(msg); } }

/** * Describes a binary search tree * Requires JDK 1.8 for Function * @author Duncan * @since 99-99-9999 * @param the data type * @see BSTreeException */ public interface BSTreeAPI> { /** * Determines whether the tree is empty. * @return true if the tree is empty; otherwise, false */ boolean isEmpty();

/** * Inserts an item into the tree. * @param obj the value to be inserted. */ void insert(E obj);

/** * Determine whether an item is in the tree. * @param item item with a specified search key. * @return true on success; false on failure. */ boolean inTree(E item);

/** * Delete an item from the tree. * @param item item with a specified search key. */ void remove(E item);

/** * returns the item with the given search key. * @param key the key of the item to be retrieved * @return the item with the specified key * @throws BSTreeException when no such element exists */ E retrieve(E key) throws BSTreeException;

/** * This function traverses the tree in in-order * and calls the function Visit once for each node. * @param func the function to apply to the data in each node */ void traverse(Function func); /** * This method returns the number of items stored in the tree. * @return the size of the tree. */ int size(); }

Sample command line text files:

smalltrees.ops

Sample command text output for smalltrees.ops: smalltrees.out

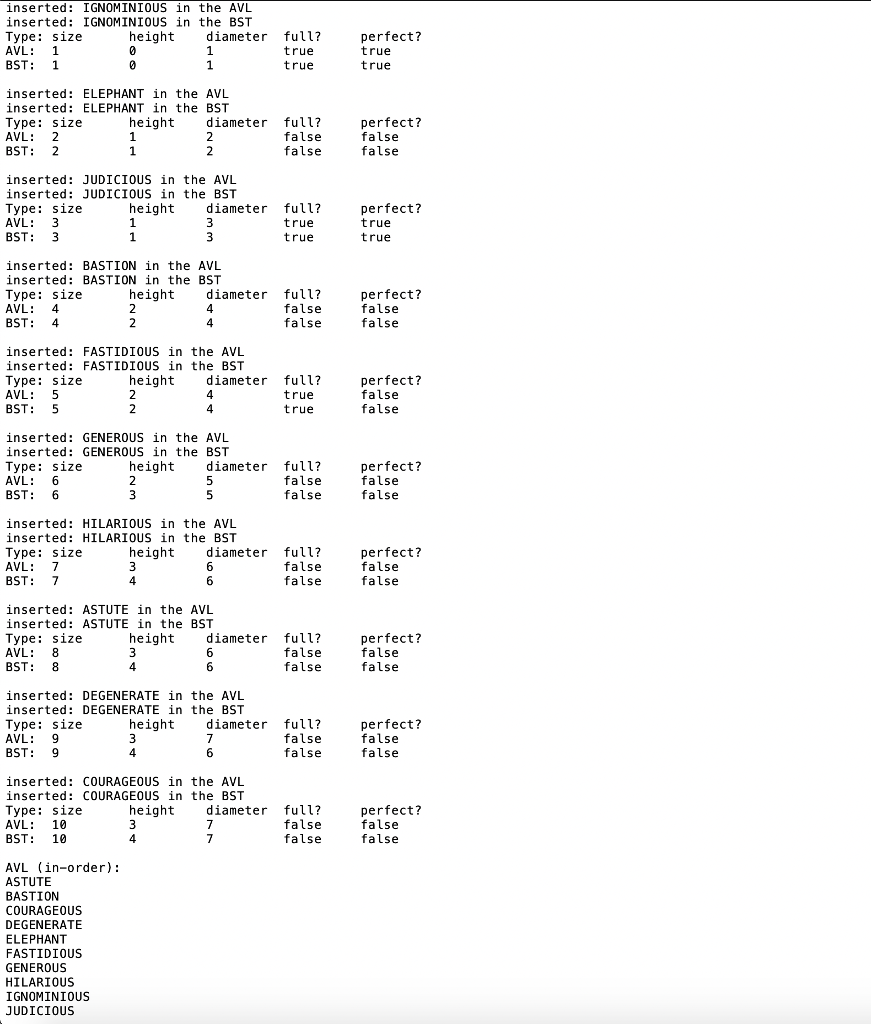
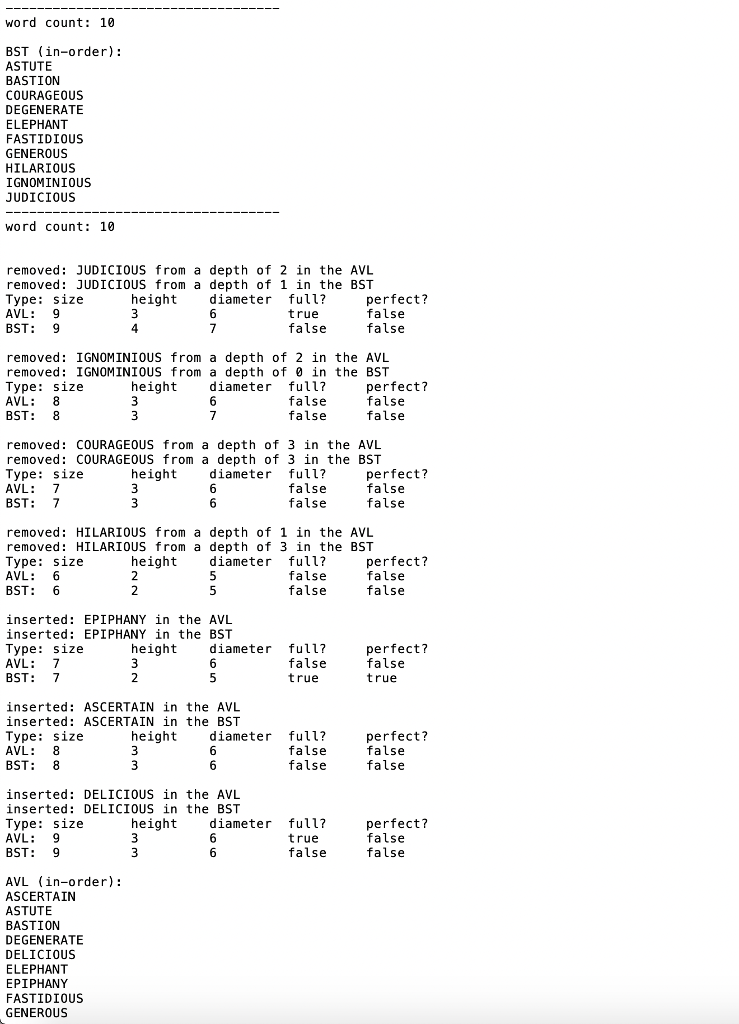
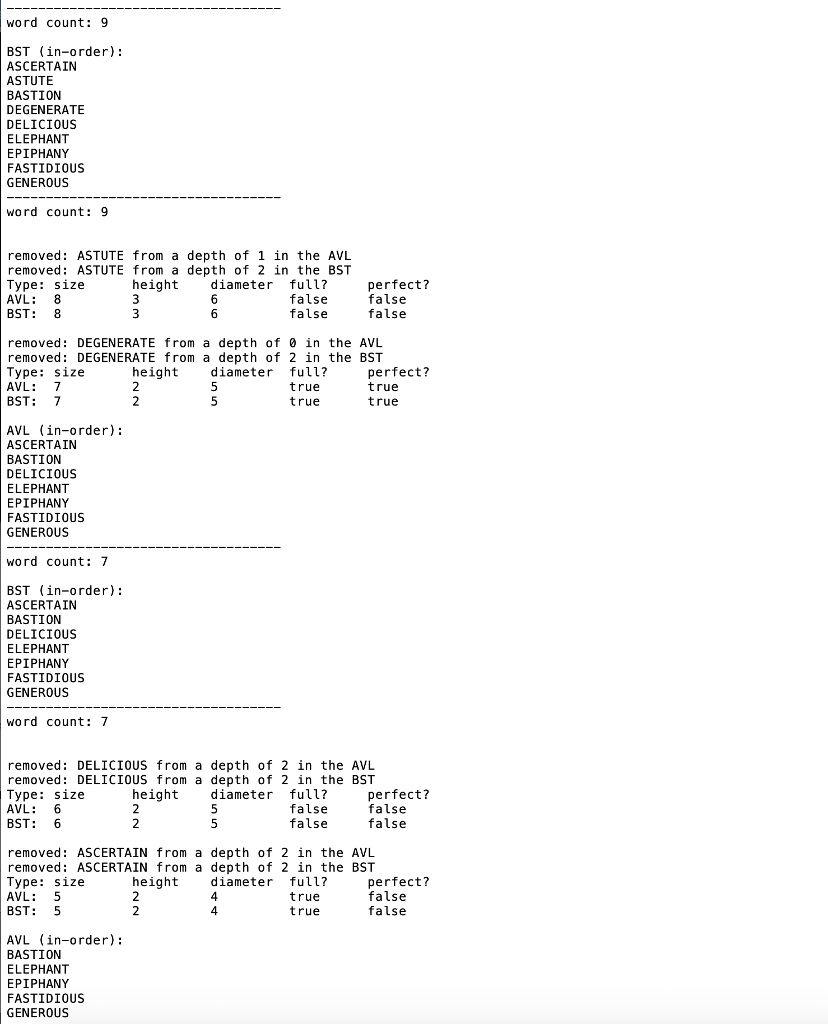
insert ignominious insert elephant insert judicious insert bastion insert fastidious insert generous insert hilarious insert astute insert degenerate insert courageous traverse remove judicious remove 1gnominlous remove courageouS remove hilarious insert epiphany insert ascertain insert delicious traverse remove astute remove degenerate traverse remove delicious remove ascertain traverse insert ignominious insert elephant insert judicious insert bastion insert fastidious insert generous insert hilarious insert astute insert degenerate insert courageous traverse remove judicious remove 1gnominlous remove courageouS remove hilarious insert epiphany insert ascertain insert delicious traverse remove astute remove degenerate traverse remove delicious remove ascertain traverse