IN MATLAB CODE PLEASE!

Part 1: Function Creation Write the functions as described in Problems 7-38 and 7-39 of your text with the following exceptions

1. Funder for problem 7-38 should be de ned as follows:

dfdx = Funder(Fun,x0,b)

Fun is a handle to a user de ned function

b is used to calculate the difference offset h at x0 using the following formula: h = x0/b

2. Both functions for Problems 7-38 and 7-39 should be written to handle vector inputs.

7-38 The first derivative df(x)/dx of a function f(x) at a point x = x0 can be approximated with the two-point central difference formula:

df(x)/dx = f(x0+h)-f(x0-h)/2h

where h is a small number relative to x0. Write a user-defined function (see Section 7.9) at calculates the derivative of a math function f(x) by using the two-point central difference formula. For the user-defined function name, use dfdx=Funder (Fun, xO), where Fun is a name for the function that is passed into Funder, and xO is the point where the derivative is calculated. Use h= x0/100 in the two-point central difference formula.

Answer:

Script file:

disp(' ') disp('Part (a)') Func=@(x) x^3*exp(2*x); dxdy=Funder(Func,0.6) disp(' ') disp('Part (b)') Func=@(x) 3^x/x^2; dxdy=Funder(Func,2.5) 

Function file:

function dfdx = Funder(Fun,x0) dfdx=(Fun(x0*1.01)-Fun(x0*.99))/(2*x0/100); 

7-39 The new coordinates (X_r, Y_r,) of a point in the x-y plane that is rotated about the z axis at an angle (degree) (positive is clockwise) are given by

X_r = X_0cos(degree)- Y_0sin(degree)

Y_2 = X_0sin=(degree)+ Y_0cos(degree) where (X_0, Y_0) are the coordinates of the point before the rotation. Write a user-defined function that calculates (X_r, Y_r) given (X_0, Y_0) and (degree). For function name and arguments, use [xr, yr] =rotation (x,y,q), where the input arguments are the initial coordinates and the rotation angle in degree and the output arguments are the new coordinates.

Answer:

Script file:

disp('Part (a)') [xnew,ynew] = rotation(6.5,2.1,25) disp(' ') disp('Part (b)') x=5:.1:9; y=(x-7).^2+1.5;

[xnew,ynew]=rotation(x,y,25);

plot(x,y,xnew,ynew,':')

title('rotation test')

legend('y=(x-7)^2+1.5','25 degree rotation')

xlabel('x-->') ylabel('y-->') axis([0 10 0 10])

Function file:

function [xr,yr] = rotation(x,y,q)

xr=x*cosd(q) -y*sind(q);

yr=x*sind(q) + y*cosd(q);

Part 2: GUI Development

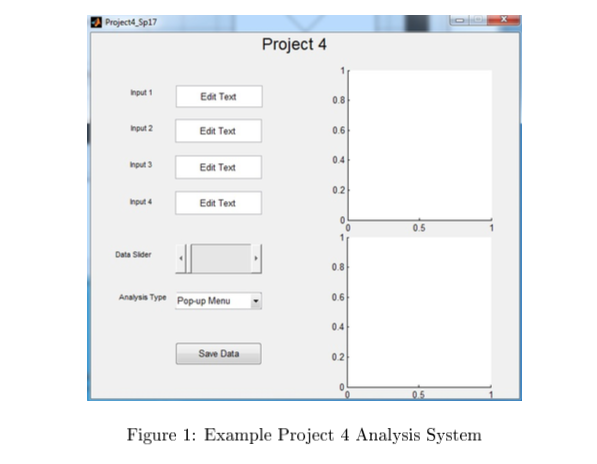
Design a general analysis system using Matlab's Graphical User Interface Design Environment (GUIDE) that completes the following analysis types:

1. Analyze the effect of the difference offset magnitude at each point.

2. Rotates an image according to the angle speci ed by the user

Difference Analysis Input 1: Function handle to be used as the input for the approximation

Input 2: Name of a vector holding the input points for the approximation Input 3: Function handle to the analytical solution of the functional derivative we are attempting to approximate. Slider Bar: Set to provide integer values for b for the F under function. Values should range from 1 to 100.

Use Inputs 1-3 and Funder you wrote in Part 1 of this project to calculate the derivative of the function speci ed in Input1 at the points speci ed in Input 2 for the individual o ets obtained from the scale factor provided by the slider bar.. Plot the results of this approximation in plot area 1.

Evaluate the analytical solution to the derivative speci ed in Input 4 at the points speci ed in Input 2. Determine the di erence between the analytical solution and the approximation. Plot the analytical solution and the magnitude of the di erence as error bars at each point in plot area 2.

Save results of the approximation, the analytical solution, and the scale factor as GUI Variables

Rotation Analysis

Input 1: Function handle to be used as the input for the image rotation. (Note: this requires a function that operates on two variables)

Input 2: Name of a vector holding the input X coordinates

Input 3: Name of a vector holding the input Y coordinates

Input 4: Function handle to the analytical solution of the functional derivative we are attempting to approximate.

Slider Bar: Set to provide integer values for for therotation function. Values should range from 1 to 359;

Calculate the output of the function speci ed in Input1 at the points speci ed in Inputs 2 and 3. Plot the results in plot area 1

Call the rotation function you wrote in Part 1 using the X and Y input coordinates given in Inputs 2 and 3 and the value from the slider bar.

Evaluate the input function using the new rotated coordinates.

Display the results in plot area 2

Save results of the input function output for the input coordinates, the rotated coordinates, function output for the rotated coordinates, and the current value as GUI Variables

Useful Functions: meshgrid and imagesc.

Analysis Type Selection The type of analysis is determined by a pop-up menu with a list of the 2 analysis types.

Save Results Button Use this button to save all the GUI variable speci ed in the Di erence and Rotation Analyses back to Matlab's base workspace.

IN MATLAB CODE PLEASE!

Project Sp17 Project 4 Input 1 Edit Text 0.8 Input 2 0.6 Edit Text Input 3 Edit Text Input 4 Edit Text Data Sider Analysis Type Popup Menu 0.6 Save Data Figure 1: Example Project 4 Analysis System Project Sp17 Project 4 Input 1 Edit Text 0.8 Input 2 0.6 Edit Text Input 3 Edit Text Input 4 Edit Text Data Sider Analysis Type Popup Menu 0.6 Save Data Figure 1: Example Project 4 Analysis System