In paper manufacturing, pulp brightness is an important performance characteristic. Customers require maximum pulp brightness with maximum uniformity (minimum variance). The company is testing two bleaching chemicals for effectiveness in achieving a brightness of 90. Assume that the data are normally distributed. (a) State and test the hypothesis that the brightness variances of the two chemicals are equal at ? = 0.05. (b) State and test the hypothesis that the brightness means for the two chemicals are equal at ? = 0.05. (c) Which chemical best fulfills the requirements of maximum brightness at minimum variance?

Using Minitab

Chemical 1 Chemical 2 90.61 89.17 90.11 85.73 89.41 93.27 90.69 88.29 89.42 95.16 88.42 87.02 90.40 89.59 90.71 87.31 89.52 87.92 89.25 96.86

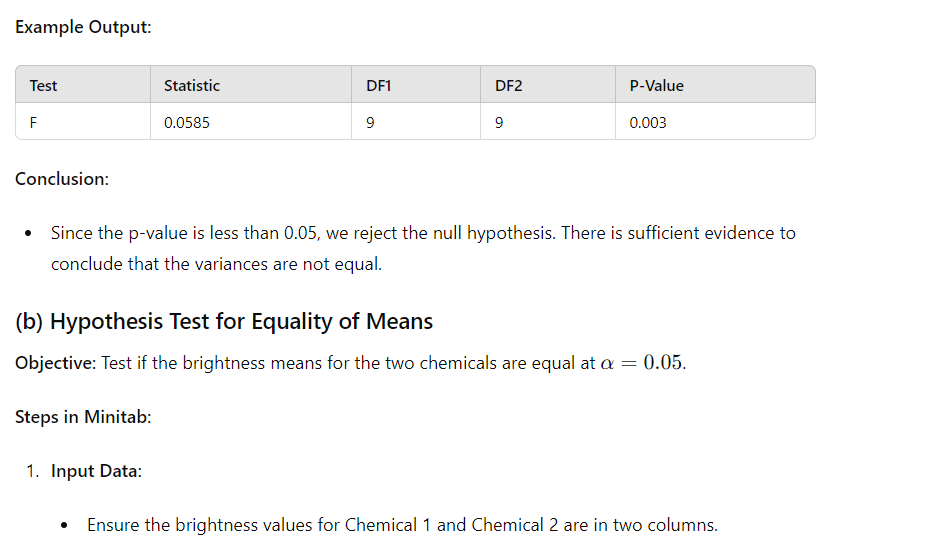
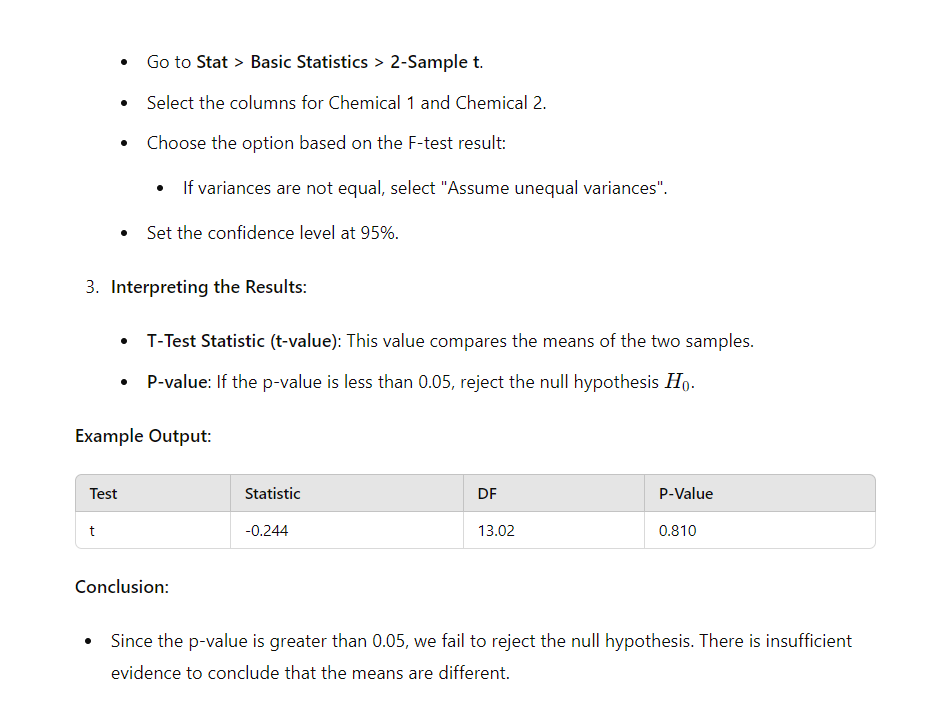
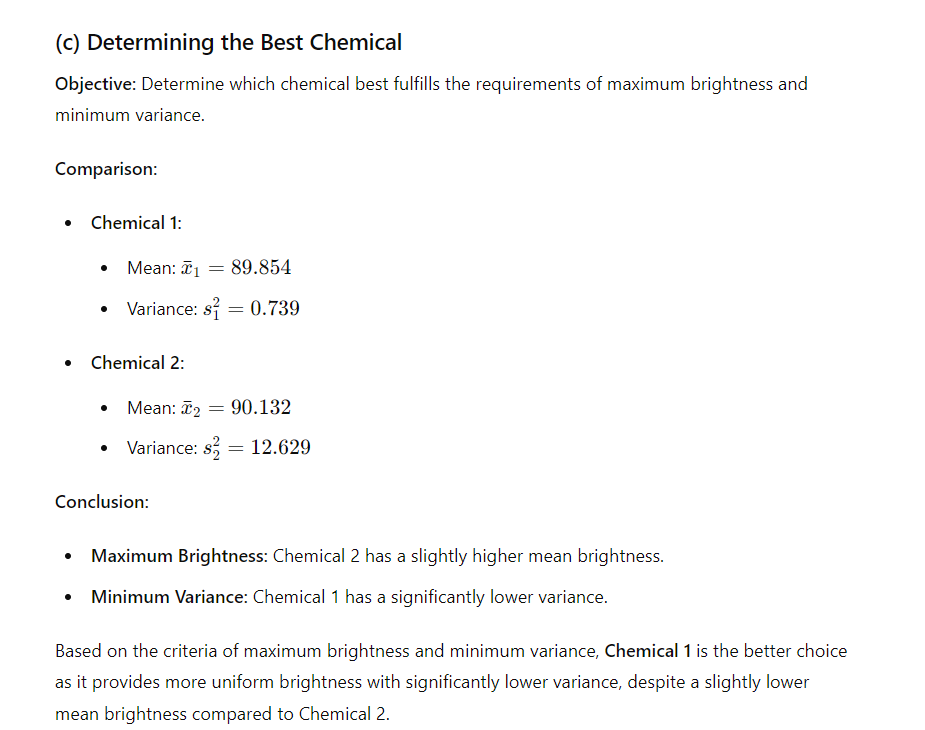(a) Hypothesis Test for Equality of Variances Objective: Test if the brightness variances of the two chemicals are equal at a = 0.05. Steps in Minitab: 1. Input Data: Enter the brightness values for Chemical 1 and Chemical 2 into two columns. 2. Perform F-Test: s (5o to Stat > Basic Statistics > 2 Variances. o Select the columns for Chemical 1 and Chemical 2. Check "Perform hypothesis test" and set the confidence level at 95%. 3. Interpreting the Results: F-Test Statistic (F-value): This value compares the variances of the two samples. * P-value: If the p-value is less than 0.05, reject the null hypothesis Hj,. Example Output: Test Statistic DF1 DF2 P-Value F 0.0585 G g 0.003 Conclusion: * Since the p-value is less than 0.05, we reject the null hypothesis. There is sufficient evidence to conclude that the variances are not equal. (b) Hypothesis Test for Equality of Means Objective: Test if the brightness means for the two chemicals are equal at a = 0.05. Steps in Minitab: 1. Input Data: Ensure the brightness values for Chemical 1 and Chemical 2 are in two columns. * (o to Stat > Basic Statistics > 2-Sample t. e Select the columns for Chemical 1 and Chemical 2. Choose the option based on the F-test result: |f variances are not equal, select "Assume unequal variances". e Set the confidence level at 95%. 3. Interpreting the Results: * T-Test Statistic (t-value): This value compares the means of the two samples. e P-value: If the p-value is less than 0.05, reject the null hypothesis Hj. Example Output: Test Statistic DF P-Value t -0.244 13.02 0.810 Conclusion: Since the p-value is greater than 0.05, we fail to reject the null hypothesis. There is insufficient evidence to conclude that the means are different. (c) Determining the Best Chemical Objective: Determine which chemical best fulfills the requirements of maximum brightness and minimum variance. Comparison: Chemical 1: e Mean: T, = 89.854 Variance: 57 = (.739 Chemical 2: e Mean: T = 90.132 e \\ariance: s% = 12.629 Conclusion: Maximum Brightness: Chemical 2 has a slightly higher mean brightness. Minimum Variance: Chemical 1 has a significantly lower variance. Based on the criteria of maximum brightness and minimum variance, Chemical 1 is the better choice as it provides more uniform brightness with significantly lower variance, despite a slightly lower mean brightness compared to Chemical 2