In Python please

Copyable code:

def printMatrix(m):

for row in m:

print(row)

def chainMatrix(dims):

# Create the empty 2-D table

n = len(dims)-1

m = [[None for i in range(n)] for j in range(n)]

# Fill in the base case values

for i in range(n):

m[i][i] = 0

# Fill in the rest of the table diagonal by diagonal

for chainLength in range(2,n+1):

for i in range(n+1-chainLength):

j = i + chainLength - 1

# Fill in m[i][j] with the best of the recursive options

m[i][j] = float("inf")

for k in range(i,j):

# Two previous table values plus

# what it cost to mult the resulting matrices

q = m[i][k]+m[k+1][j]+dims[i]*dims[k+1]*dims[j+1]

if q

m[i][j] = q

printMatrix(m)

return m[0][n-1]

dims = [30,35,15,5,10,20,25]

print(chainMatrix(dims))

I got the optimal table and the traceback table to show the right outputs. I need help with the traceback please.

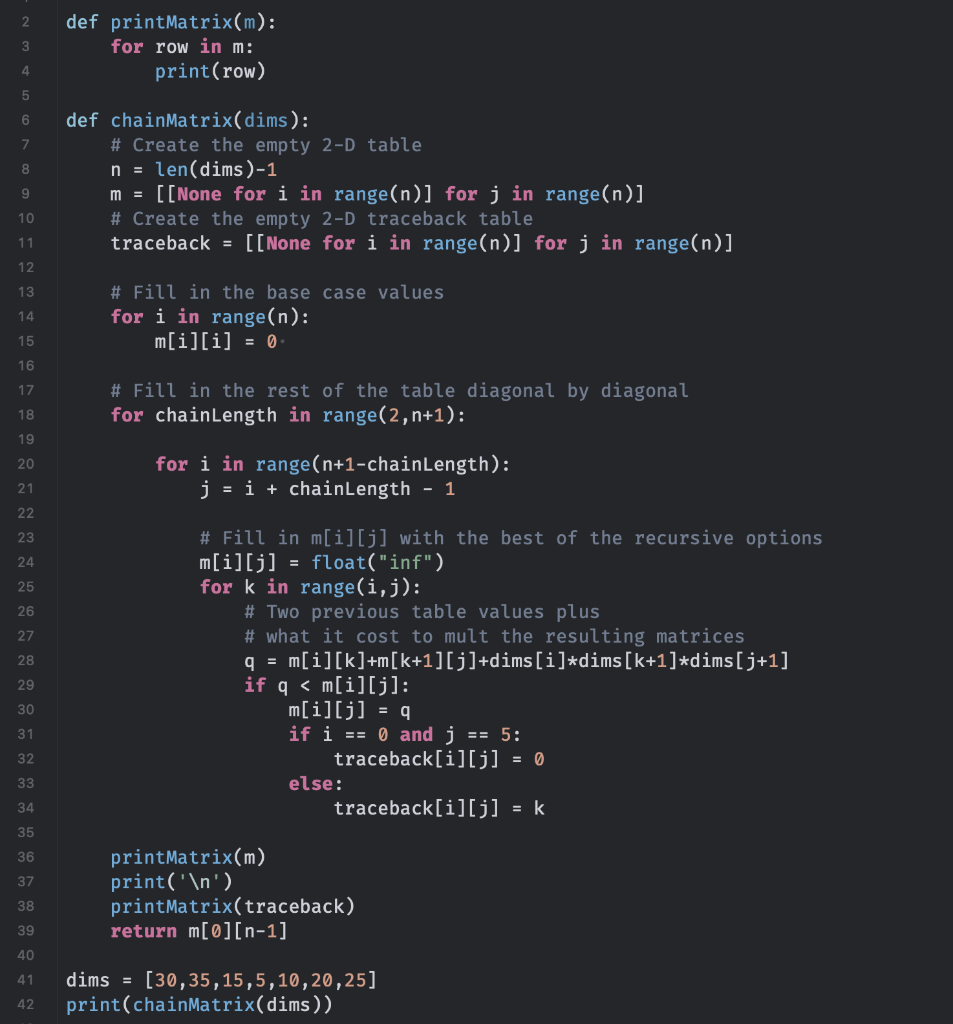
Chained Matrix Multiplication DP Below is code to solve the chained matrix multiplication problem using dynamic programming. The dims parameter it takes is a list of the dimensions of the matrices to be multiplied. For example, if Ao is a 10 x 15, A1 is a 15 x 8, and A2 is an 8 x 3, then dims would be [10, 15, 8, 3] because the inner dimensions must match during multiplication. It returns the optimal cost of the full multiplication. Also included in the code is a function to print out the optimal cost matrix. It is called only once right now, but I would suggest printing at a number of different locations if you want to follow what the code is doing. The code as given produces only the optimal table and can tell you the optimal cost. If you want to know how to actually apply the parentheses, then you need to produce a traceback table and apply that table to the matrices. This is your task in this lab. The first thing you need to do is to add the creation of the traceback table to the chainMatrix function. Second, define a new function called parenStr that will return a string representation of the matrices with parentheses. You should call this function and print out the resulting string as the last thing you do in chainMatrix before it returns. parenStr will obviously need parameters, but I'm leaving it up to you to figure what to pass. Note that this function will most likely be a recursive function. Note that the example hard-coded below is similar to the one from the video/PowerPoint slides. However, there was a slight mistake in the video/PowerPoint slides' tables. The traceback table value for (0,5) is listed as a 0 when it should really be a 2. This, unfortunately, has an impact on the placing of parentheses as well because that value is used. So, although the video correctly describes the procedure, it uses a wrong value and thus comes up with the wrong answer. The correct answer you should come produce with your code is: ((A0) ((A1) (A2))) (((A3) (A4)) (A5)) 2 3 def printMatrix(m): for row in m: print(row) 4 5 6 7 8 def chainmatrix(dims): # Create the empty 2-D table n = len(dims)-1 m = [[None for i in range(n)] for j in range(n)] # Create the empty 2-D traceback table traceback = [[None for i in range(n)] for j in range(n)] 9 10 11 12 13 14 # Fill in the base case values for i in range(n): m[i][i] = 0 15 16 17 # Fill in the rest of the table diagonal by diagonal for chainLength in range(2,n+1): 18 19 20 for i in range(n+1-chainLength): j = i + chainLength - 1 21 22 23 24 25 26 27 28 29 30 # Fill in m[i][j] with the best of the recursive options m[i][j] = float("inf") for k in range(i,j): # Two previous table values plus # what it cost to mult the resulting matrices q = m[i][k]+m[k+1][j]+dims[i]*dims[k+1]*dims[j+1] if q