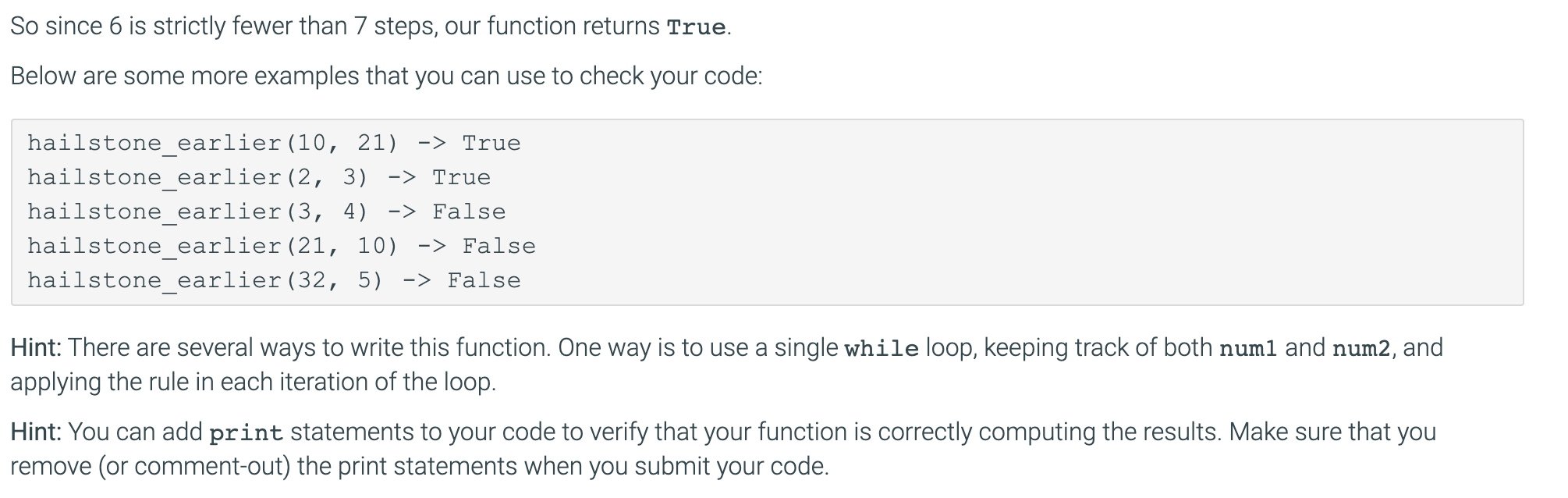
in python please

One currently unsolved problem in mathematics looks at sequences of numbers, sometimes called hailstone numbers. The way to get from one hailstone number to the next one is simple: If it's even, divide it by 2. If it's odd, multiply it by 3 and add 1. From any starting number, you can make a sequence of numbers, applying this rule repeatedly. Mathematicians guess that if you apply the rule enough times to any natural number, you'll eventually end up with 1 (which then is tripled plus one to get 4, then 2, then 1 again in an endless cycle). The formalization of this guess is called the Collatz Conjecture, and it is one of the most well-known open problems. Your task is: Given any two positive integers num1 and num2, write a function that returns True if the sequence of hailstone numbers starting with num1 takes fewer steps to get to 1 than the sequence starting with num2; otherwise, the function returns False. Let's look at hailstone_earlier(10, 21) which should return True. In this case, num1 is 10 and num2 is 21. First, let's look at num1: since 10 is even, we can get the next number by dividing it by 2, so 10/2=5 since 5 is odd, the next number is 5*3+1 = 16 then 16/2 = 8, then 8/2 = 4, . then 4/2 = 2 then 2/2 = 1, and we've arrived at 1 in 6 steps. Then, let's look at num2: since 21 is odd, the next number is 21*3+1 = 64 since 64 is even, the next number is 64/2 = 32 then 32/2 = 16, then 16/2 = 8, then 8/2 = 4, . then 4/2 = 2 then 2/2 = 1, and we've arrived at 1 in 7 steps. So since 6 is strictly fewer than 7 steps, our function returns True. Below are some more examples that you can use to check your code: hailstone_earlier (10, 21) -> True hailstone_earlier (2, 3) -> True hailstone_earlier (3, 4) -> False hailstone_earlier (21, 10) -> False hailstone_earlier (32, 5) -> False Hint: There are several ways to write this function. One way is to use a single while loop, keeping track of both num1 and num2, and applying the rule in each iteration of the loop. Hint: You can add print statements to your code to verify that your function is correctly computing the results. Make sure that you remove (or comment-out) the print statements when you submit your code