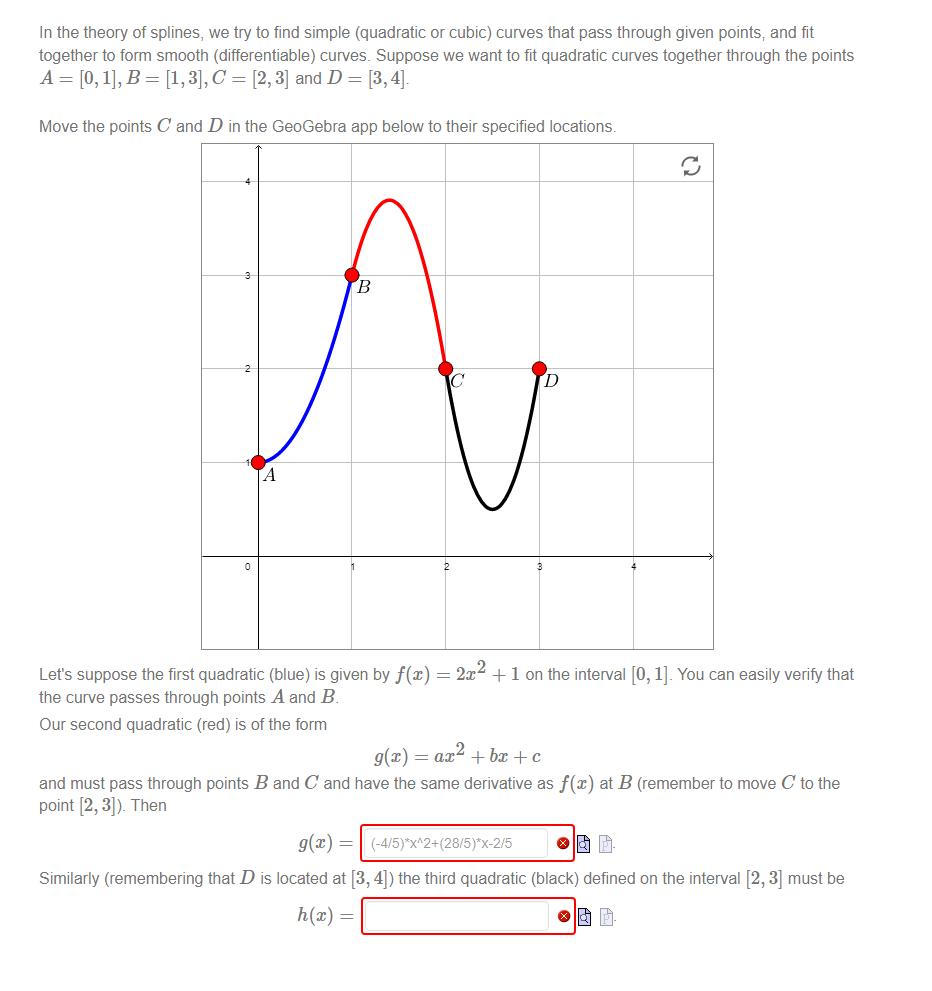
In the theory of splines, we try to find simple (quadratic or cubic) curves that pass through given points, and fit together to form smooth (differentiable) curves. Suppose we want to fit quadratic curves together through the points A [0,1], B = [1,3], C= [2,3] and D = [3,4]. Move the points C and D in the GeoGebra app below to their specified locations. 3 B A Let's suppose the first quadratic (blue) is given by f(x) = 2x + 1 on the interval [0, 1]. You can easily verify that the curve passes through points A and B. Our second quadratic (red) is of the form g(x) = ax + bx + c and must pass through points B and C and have the same derivative as f(x) at B (remember to move C to the point [2, 3]). Then g(x)=(-4/5)*x^2+(28/5)*x-2/5 Similarly (remembering that D is located at [3, 4]) the third quadratic (black) defined on the interval [2, 3] must be h(x) =