In this assignment, we implement a five-card poker game. This is how the program works:

One of the players is the user, while the other is the computer. In the first round (and all the odd rounds), the player must initially bet a certain amount before seeing their hand. In the second round (and all the even rounds), the computer must bet initially. The amount of bet is deducted from the better's account and is added to the pot. Then, the program assigns five cards to both players randomly. A pop-up window must show the hand of the user, the total money in the pot, and the player's balance. If it is an even round, the user is asked to enter their bet. The value of the bet can be any amount from 0 to player's balance. The computer, then, decides to quit (fold), accept (call), or even increase (raise) the bet based on its hand, its current total, and the player's bet. There are three possibilities:

If the computer gives up, the player wins the round. The money (pot) is added to player's account.

If it accepts the bet, a new window must appear that shows the user's hand and the computer's hand. The one with the better hand wins the prize. The money is added to the winner's account.

If the computer raises the bet, a new window appears. This window shows the total money in the pot, the total amount of computer's raise, and the user's hand. The user can fold by entering 0. They can call by entering the difference. They cannot raise anymore, though. Then a window showing both hands appears. The one with the better hand wins the prize. The odd rounds are similar. The only difference is that computer makes the first move. The game continues until the balance of one of the players reaches zero. That player is the looser.

The computer must be able to assess its hand and act based on the cards it has. Refer to the link below to learn more about poker hands: Link: https://en.wikipedia.org/wiki/List_of_poker_hands

As you can see, there are ten different hands in poker (Ignore five of a kind as we do not use Joker). You need to think of an algorithm to assess and score each hand. First, you need to find if it is high card, one pair, two pair, etc. This is not a difficult task as there are only nine different hands in poker that we care about. Then you assign the hand an absolute numerical value. Consider the examples below:

Let's say we evaluate a hand and we realize it is a High Card. The value of that hand is the value of the most important card. If the highest card is 10 of Spades, then the value of that card is 10. If it is King of Diamonds, then the value is 13. If it is Ace of Clubs, then the value of the hand is 14.

Let's say we evaluate a hand and we realize it is a One Pair. We know that this hand must beat even the best High Card hand. Therefore, the value of the worst One Pair hand (a pair of twos) must be higher than the value of the best High Card hand (Ace). Consequently, we should assign 14 (the value of Ace) + 2 (because it is a pair of twos) to that hand. If we have a pair of Queens, then the value of that hand must be 14 + 12. Using this algorithm, it is clear than a pair of tens (14+10) beats a pair of fives (14+5). The most valuable One Pair hand is a pair of Aces. The value of this hand is 14+14=28.

Let's say we evaluate a hand and we realize it is a Two Pair. We know that even the worst Two Pair beats the best One Pair. Therefore, the value of the worst two pair (a pair of twos and a pair of threes) must be higher than the value of the best One Pair (which is a pair of Aces with the value of 28). One solution is to use 28+pair1+pair2. This, however, does not work. Because according to that formula, a pair of Aces and a pair of twos gets (28+14+2=44), while a pair of Kings and a pair of Queens gets (28+13+12=53). This means that latter beats the former, which is wrong. We can fix it by adding a coefficient to the highest pair of the two pairs. That coefficient must be at least 11 (why?). However, I prefer to use 20. Therefore, we can use this formula: 28+20highestPair+lowestPair. Using this formula, a pair of Aces and a pair of twos gets 28+2014+2=310, while a pair of Kings and a pair of Queens gets 28+2013+12=300. The best Two Pair Hand is a pair of Aces and a pair of Kings, which gets 28+2014+13=321.

Lets say we evaluate a hand and we realize it is a Three of a Kind. We know that the weakest Three of a Kind (which consists of three twos) beats the best Two Pair (and consequently One Pair and High Card). Using the same logic, we can infer that the following formula is good enough: 321+the value of the card. For example, a hand with three nines gets the value of 321+9=330. The best Three of a Kind gets 321+14=335.

You can go ahead and evaluate all hands in a similar manner.

You program must be smart enough to determine when to fold, when to call, and when to raise. Doing this properly is difficult. In this program, we use a simple approach. Define a variable called riskFactor. We need to come up with a formula for this one. The riskFactor is determined based on the value of the hand, the total money in the pot, and players balance. We can use a formula like this:

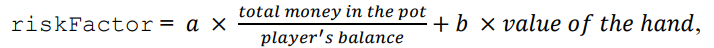
where b is a negative constant and a is a positive one. Adjust these values to come with a good formula.

Program Structure.

You need to create a class called Player. This class has a data member for balance and a data member for hand, which consists of five cards. It is up to you to determine what functions you need in this class. It is also up to you to determine if they need to be public, protected, or private. If you make data member or a member method public, without having a convincing reason, you will lose points.

You also need a class called Card. It is up to you to determine the data members and member methods.

You need a class for Deck.

You also need a class called Game, which handles everything. This class has two objects of class Player and an object of class Deck. The main method must be part of this class.

You know that bluffing is very common in poker. We do not want the computer to be rational all the time, as it makes it very predictable. Make the computer bluff 3-4% of the times, meaning that even if the computer doesn't have a good hand it should not always fold sometimes, when the computer is dealt a bad hand, it should pretend it was dealt a good hand to make the game more realistic.

total money in the pot player's balance b value of the hand