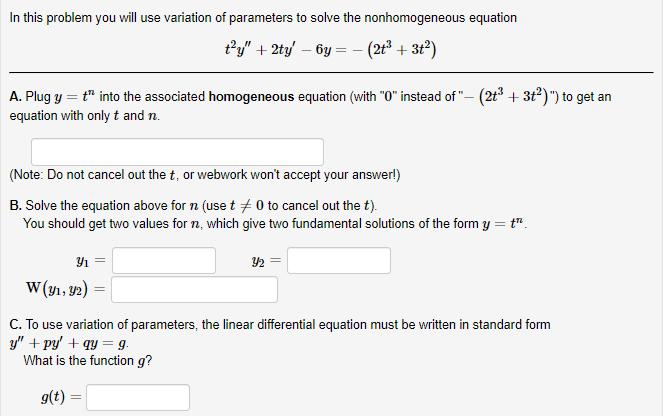
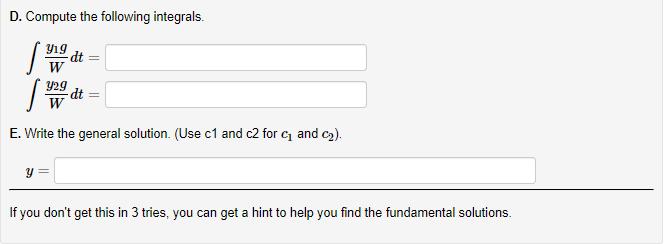
In this problem you will use variation of parameters to solve the nonhomogeneous equation t'y" + 2ty 6y = - (2t + 3t) A. Plug y = t" into the associated homogeneous equation (with "0" instead of "- (2t + 3t2)") to get an f". equation with only t and n. (Note: Do not cancel out the t, or webwork won't accept your answerl) B. Solve the equation above for n (use t +0 to cancel out the t). You should get two values for n, which give two fundamental solutions of the form y = t". Y1 = W (y1, 2) = C. To use variation of parameters, the linear differential equation must be written in standard form y" + py' + qy = g. What is the function g? g(t) : D. Compute the following integrals. Y19 dt W Y29 dt W E. Write the general solution. (Use c1 and c2 for c and c2). If you don't get this in 3 tries, you can get a hint to help you find the fundamental solutions.