In this problem, you will write a program that solves Sudoku puzzles using recursive backtracking.

Overview A Sudoku puzzle consists of a 9x9 grid in which some of the cells have been filled with integers from the range 1-9. To solve the puzzle, you fill in the remaining cells with integers from the same range, such that each number appears exactly once in each row, column, and 3x3 subgrid.

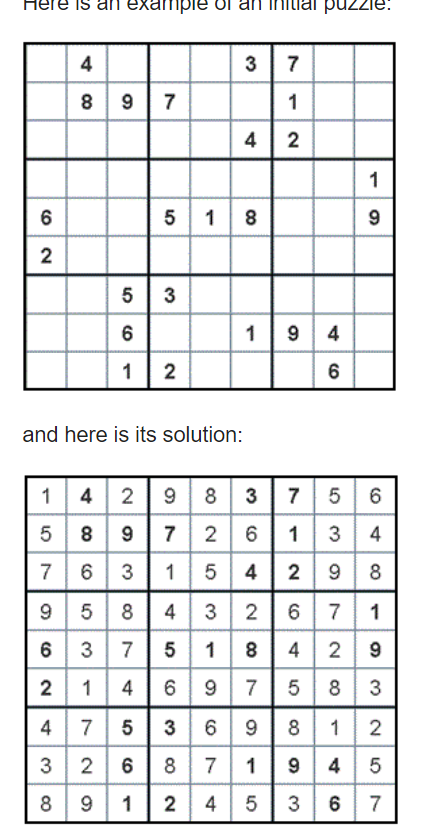
Here is an example of an initial puzzle:

In this problem, you will write a program that solves Sudoku puzzles using recursive backtracking.

Overview A Sudoku puzzle consists of a 9x9 grid in which some of the cells have been filled with integers from the range 1-9. To solve the puzzle, you fill in the remaining cells with integers from the same range, such that each number appears exactly once in each row, column, and 3x3 subgrid.

Here is an example of an initial puzzle:

In this problem, you will write a program that solves Sudoku puzzles using recursive backtracking.

Overview A Sudoku puzzle consists of a 9x9 grid in which some of the cells have been filled with integers from the range 1-9. To solve the puzzle, you fill in the remaining cells with integers from the same range, such that each number appears exactly once in each row, column, and 3x3 subgrid.

Here is an example of an initial puzzle:

Most of the functionality of your program should go in a class called Puzzle, which you will use to represent an individual Sudoku puzzle. We have provided you with skeleton code for this class in the file Puzzle.java, which you should download and modify. The provided code includes:

• a field called values that refers to a two-dimensional array of integers. This array is used to store the current contents of the cells of the puzzle, such that values[r][c] stores the current value in the cell at row r, column c of the puzzle. A value of 0 is used to indicate a blank cell.

• a field called valIsFixed that refers to a two-dimensional array of booleans. It is used to record whether the value in a given cell is fixed (i.e., part of the original puzzle). valIsFixed[r][c] is true if the value in the cell at row r, column c is fixed, and valIsFixed[r][c] is false if the value in that cell is not fixed. For example, in the original puzzle above, there is a fixed 4 in the cell at row 0, column 1 (the second cell in the top row), and thus valIsFixed[0][1] would be true for that puzzle.

• a field called subgridHasValue that refers to a three-dimensional array of booleans. This array allow us to determine if a given 3x3 subgrid of the puzzle already contains a given value. For example, subgridHasValue[0][0][4] will be true if the 3x3 subgrid in the upper left-hand corner of the board (a subgrid that we are identifying using the indices [0][0]) already has a 4 in one of its cells. See the comments accompanying this field for more information about the numbering of the subgrids.

• partial implementations of methods called placeValue() and removeValue() that place a value in a given cell and remove a value from a given cell by updating the fields mentioned above. You will need to add code to these methods to update the other fields that you add.

• a full implementation of a method called readFrom() that takes a Scanner as its only parameter and reads in a specification of a puzzle from that Scanner. This method assumes that a puzzle specification consists of nine lines of text one for each row of the puzzle and that each line contains nine digits separated by whitespace. Here again, 0 is used to indicate a blank cell. For example, the specification of the initial puzzle above would begin:

  0 4 0 0 0 3 7 0 0 0 8 9 7 0 0 1 0 0 ... 

  The method reads in the puzzle specification and makes the corresponding changes to the fields mentioned above. You should not need to change this method, because it calls placeValue(), and you are already modifying that method as needed. However, we do recommend that you read this method over.

• the full implementation of a method called display() that prints out the current state of the Puzzle object on which it is invoked.

• the skeleton of a private method called solveRB() that you will implement. This is the recursive-backtracking method, and it should return true if a solution to the puzzle is found and false if no solution has been found (i.e., if the method is backtracking). If the initial call to this method returns false, that means that no solution can be found i.e., that the initial puzzle is not valid. If there is more than one solution (which can happen if the initial puzzle does not have enough numbers specified), your code should stop after finding one of them.

  Each invocation of the solveRB() method is responsible for finding the value of a single cell of the puzzle. The method takes a parameter n, which is the number of the cell that the current invocation of this method is responsible for. We recommend that you consider the cells one row at a time, from top to bottom and left to right, which means that they would be numbered as follows:

  0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 ... 

• the full implementation of a public wrapper method called solve() that makes the initial call to solveRB(), and that returns the same value that solveRB() returns.

• a partial implementation of a constructor. You will need to add code to initialize the fields that you add.

In addition to completing the methods mentioned above, you should also add to the Puzzle class whatever additional fields or methods that are needed to efficiently maintain the state of a Sudoku puzzle and to solve it using recursive backtracking. In particular, we recommend adding two fields: one to keep track of whether a given row already contains a given value, and one to keep track of whether a given column already contains a given value. When adding these fields, make sure that you employ proper encapsulation.

For full credit, your constraint-checking must be done without scanning through the rows and columns of the Sudoku board. For example, to determine if the current column contains a 5, you should not need to look at the other cells in the current column.

We are also providing:

• a separate Sudoku class in the file Sudoku.java. It contains the main() method for your Sudoku solver. You shouldnt need to change this method (or any other code in this file), but we encourage you to review its use of the methods of the Puzzle class. In particular, note that it displays the puzzle after the solution is found, and thus your recursive-backtracking method should not display it.

• a collection of four sample puzzle files. Download this zip file, and extract its contents into the same folder as your code for this problem. The puzzles include:

  • two puzzles with only one solution (puzzle1.txt and puzzle2.txt)
  • no_solution.txt, which has no solution
  • multi_sol.txt, which has multiple solutions.

Additional hints and suggestions:

• Take advantage of the first template in the notes for recursive backtracking the one in which only one solution is found.

• As mentioned above, the recursive solveRB() method takes a single parameter n that represents the number of the cell that the current invocation is responsible for. You will need to use n to compute the row and column indices of the cell, and you should be able to do so using simple arithmetic operations (+, -, *, /, and %).

• Make sure that you take advantage of the subgridHasValue field along with the fields that you will add to keep track of the values in a given row and a given column of the puzzle when deciding whether a particular value can be assigned to a particular cell. As mentioned above, you should not scan through the puzzle to determine if a given value is valid. See our n-Queens solver for for another example of efficient constraint checking.

• Make sure that you use the addValue() and removeValue() methods when updating the state of the puzzle, and that you add code to these methods as needed to update the fields that you add to the Puzzle class.

• Make sure that you dont attempt to assign a new number to cells that are filled in the original puzzle i.e., cells whose values are fixed. Your solveRB() method will need to skip over these cells somehow.

A sample run of the program is shown below.

Enter the name of the puzzle file: puzzle1.txt Here is the initial puzzle: ------------------------------------- | | 4 | | | | 3 | 7 | | | ------------------------------------- | | 8 | 9 | 7 | | | 1 | | | ------------------------------------- | | | | | | 4 | 2 | | | ------------------------------------- | | | | | | | | | 1 | ------------------------------------- | 6 | | | 5 | 1 | 8 | | | 9 | ------------------------------------- | 2 | | | | | | | | | ------------------------------------- | | | 5 | 3 | | | | | | ------------------------------------- | | | 6 | | | 1 | 9 | 4 | | ------------------------------------- | | | 1 | 2 | | | | 6 | | ------------------------------------- Here is the solution: ------------------------------------- | 1 | 4 | 2 | 9 | 8 | 3 | 7 | 5 | 6 | ------------------------------------- | 5 | 8 | 9 | 7 | 2 | 6 | 1 | 3 | 4 | ------------------------------------- | 7 | 6 | 3 | 1 | 5 | 4 | 2 | 9 | 8 | ------------------------------------- | 9 | 5 | 8 | 4 | 3 | 2 | 6 | 7 | 1 | ------------------------------------- | 6 | 3 | 7 | 5 | 1 | 8 | 4 | 2 | 9 | ------------------------------------- | 2 | 1 | 4 | 6 | 9 | 7 | 5 | 8 | 3 | ------------------------------------- | 4 | 7 | 5 | 3 | 6 | 9 | 8 | 1 | 2 | ------------------------------------- | 3 | 2 | 6 | 8 | 7 | 1 | 9 | 4 | 5 | ------------------------------------- | 8 | 9 | 1 | 2 | 4 | 5 | 3 | 6 | 7 | -------------------------------------

example puzzle: 3 7 4 8 9 7 1 4 2 1 6 51 18 9 2 53 6 1 94 1 N 6 and here is its solution: 1 4 2 9 8 37 56 5 8 9 7 2 6 1 3 4 7 6 31 5 4 2 9 8 9 9 5 8 4 3 2 6 7 1 6|3|75|1|8|4|2|9 2 1 4 6 9 7 5 8 3 4 7 5 3 6 9 8 1 2 2 68 7 2 4 4 5 4 3 1 9 4 5 8 9 1 3 6 7