
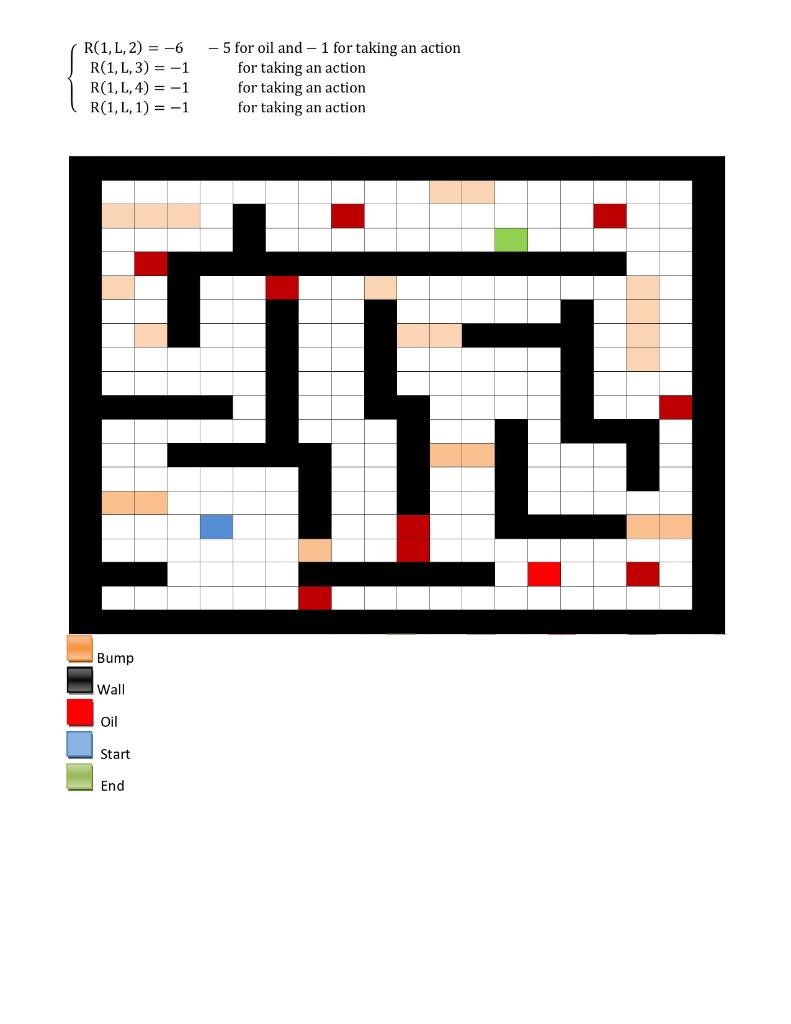

In this project, we consider a maze shown on the second page. This maze consists of several walls that the agent cannot enter, and bumps and oils that moving to them have negative rewards. For simplicity, consider an 1818 matrix, where each element is associated with one of the following: - Empty - Full (Wall) - Bump - Oil State Space (S): The state-space contains all cells in the maze except the walls, where the agent can possibly be there (181876( walls )=248). Action Space (A): The agent can take one of the four possible actions at any given state: up (U), down (D), right (R), and left (L). Transition Probabilities: After choosing an action, the agent will either move to one of the neighborhood cells or stay in its current cell. After taking any action, with a probability of 1-p, the agent moves to the anticipated state and, with an equal probability of p/3, will move to one of the other neighboring cells (or remain in the same state if any neighboring cell is not a feasible state). Consider the following example: If action right (R) is selected, the agent: movestothestateinrightwithprobability1pmovestothestateinleftwithprobabilityp/3movestothethestateinupwithprobabilityp/3movestothestateindownwithprobabilityp/3 Notice that if any of the neighboring cells are wall, the agent stays in the current cell. Reward Function: The primary objective is to find the optimal policy which leads the agent to the goal state with the maximum accumulated reward. Therefore, we define the reward of taking any action -1 , the reward for ending up to the oil states -5 , the reward for ending up the bump states -10 , and the reward for the goal state +200 . For instance, this can be expressed for the following example as: R(1,L,2)=6R(1,L,3)=1R(1,L,4)=1R(1,L,1)=15foroiland1fortakinganactionfortakinganactionfortakinganactionfortakinganaction Implement this environment in Python and develop an API to visualize the maze. Implement a random walk policy (choosing all four possible actions equaly-likely in any state), which terminates after T=500 steps. Plot the distribution of the total reward you receive from 100 runs. In this project, we consider a maze shown on the second page. This maze consists of several walls that the agent cannot enter, and bumps and oils that moving to them have negative rewards. For simplicity, consider an 1818 matrix, where each element is associated with one of the following: - Empty - Full (Wall) - Bump - Oil State Space (S): The state-space contains all cells in the maze except the walls, where the agent can possibly be there (181876( walls )=248). Action Space (A): The agent can take one of the four possible actions at any given state: up (U), down (D), right (R), and left (L). Transition Probabilities: After choosing an action, the agent will either move to one of the neighborhood cells or stay in its current cell. After taking any action, with a probability of 1-p, the agent moves to the anticipated state and, with an equal probability of p/3, will move to one of the other neighboring cells (or remain in the same state if any neighboring cell is not a feasible state). Consider the following example: If action right (R) is selected, the agent: movestothestateinrightwithprobability1pmovestothestateinleftwithprobabilityp/3movestothethestateinupwithprobabilityp/3movestothestateindownwithprobabilityp/3 Notice that if any of the neighboring cells are wall, the agent stays in the current cell. Reward Function: The primary objective is to find the optimal policy which leads the agent to the goal state with the maximum accumulated reward. Therefore, we define the reward of taking any action -1 , the reward for ending up to the oil states -5 , the reward for ending up the bump states -10 , and the reward for the goal state +200 . For instance, this can be expressed for the following example as: R(1,L,2)=6R(1,L,3)=1R(1,L,4)=1R(1,L,1)=15foroiland1fortakinganactionfortakinganactionfortakinganactionfortakinganaction Implement this environment in Python and develop an API to visualize the maze. Implement a random walk policy (choosing all four possible actions equaly-likely in any state), which terminates after T=500 steps. Plot the distribution of the total reward you receive from 100 runs









