public class MyAVLTreeMap extends TreeMap {

/** Constructs an empty map using the natural ordering of keys. */
public MyAVLTreeMap() { super(); }

/**
* Constructs an empty map using the given comparator to order keys.
* @param comp comparator defining the order of keys in the map
*/
public MyAVLTreeMap(Comparator comp) { super(comp); }

/** Returns the height of the given tree position. */
protected int height(Position> p) {
return tree.getAux(p);
}

/** Recomputes the height of the given position based on its children's heights. */
protected void recomputeHeight(Position> p) {
tree.setAux(p, 1 + Math.max(height(left(p)), height(right(p))));
}

/** Returns whether a position has balance factor between -1 and 1 inclusive. */
protected boolean isBalanced(Position> p) {
return Math.abs(height(left(p)) - height(right(p))) <= 1;
}

/** Returns a child of p with height no smaller than that of the other child. */
protected Position> tallerChild(Position> p) {
if (height(left(p)) > height(right(p))) return left(p); // clear winner
if (height(left(p)) < height(right(p))) return right(p); // clear winner
// equal height children; break tie while matching parent's orientation
if (isRoot(p)) return left(p); // choice is irrelevant
if (p == left(parent(p))) return left(p); // return aligned child
else return right(p);
}

/**
* Utility used to rebalance after an insert or removal operation. This traverses the
* path upward from p, performing a trinode restructuring when imbalance is found,
* continuing until balance is restored.
*/
protected void rebalance(Position> p) {
int oldHeight, newHeight;
do {
oldHeight = height(p); // not yet recalculated if internal
if (!isBalanced(p)) { // imbalance detected
// perform trinode restructuring, setting p to resulting root,
// and recompute new local heights after the restructuring
p = restructure(tallerChild(tallerChild(p)));
recomputeHeight(left(p));
recomputeHeight(right(p));
}
recomputeHeight(p);
newHeight = height(p);
p = parent(p);
} while (oldHeight != newHeight && p != null);
}

/** Overrides the TreeMap rebalancing hook that is called after an insertion. */
@Override
protected void rebalanceInsert(Position> p) {
rebalance(p);
}

/** Overrides the TreeMap rebalancing hook that is called after a deletion. */
@Override
protected void rebalanceDelete(Position> p) {
if (!isRoot(p))
rebalance(parent(p));
}

/** Ensure that current tree structure is valid AVL (for debug use only). */
private boolean sanityCheck() {
for (Position> p : tree.positions()) {
if (isInternal(p)) {
if (p.getElement() == null)
System.out.println("VIOLATION: Internal node has null entry");
else if (height(p) != 1 + Math.max(height(left(p)), height(right(p)))) {
System.out.println("VIOLATION: AVL unbalanced node with key " + p.getElement().getKey());
dump();
return false;
}
}
}
return true;
}

public void printTree() {
// Put your code to print AVL tree here
System.out.println("Print of tree");
}

}
public class ProgProject4 {
public static void main(String[] args) {
String[] inputs = {
"CBDAE",
"DACBEFMLGHJK",
"JABCDEFISN"
};
for (int k=0; kMyAVLTreeMap mytree = new MyAVLTreeMap();
// this code populates your tree
for (int i =0 ; i< inputs[k].length(); i++) {
mytree.put(inputs[k].substring(i,i+1), 1);
}
System.out.println("Input of " + inputs[k]);
// this line of code call the printTree method you are to write
mytree.printTree();
System.out.println();


}

}
}
 

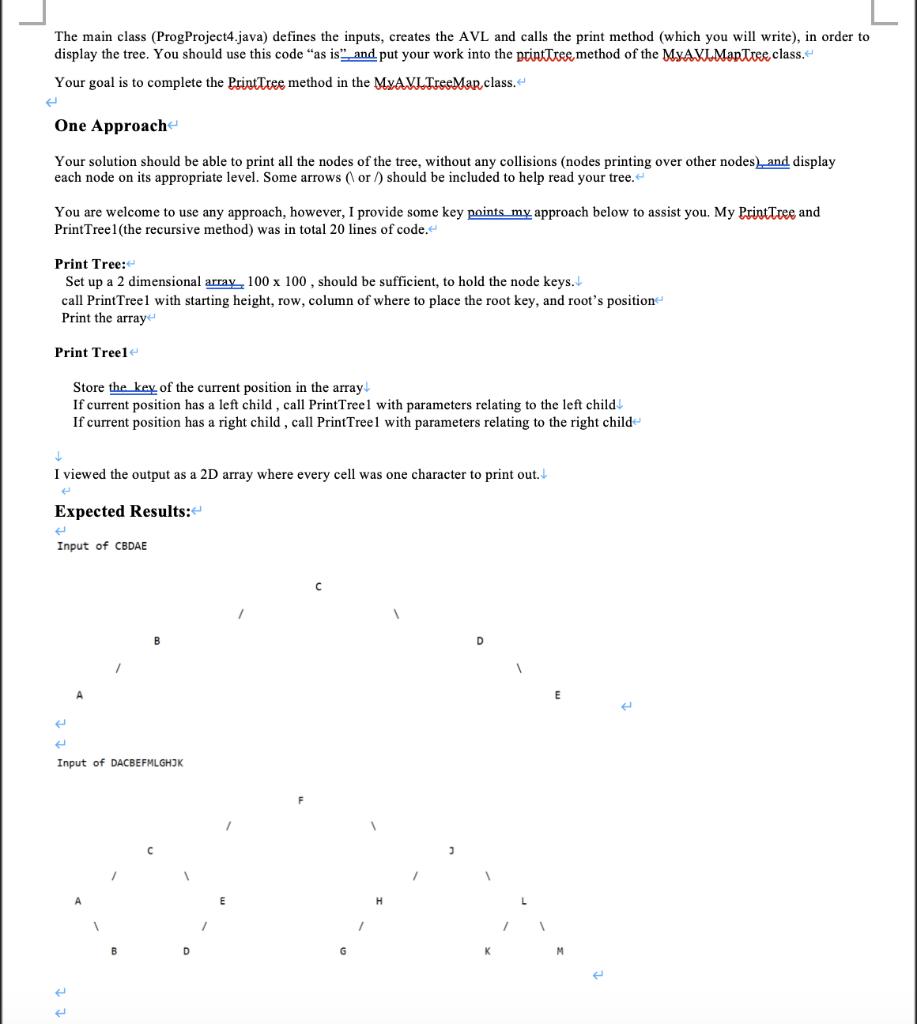
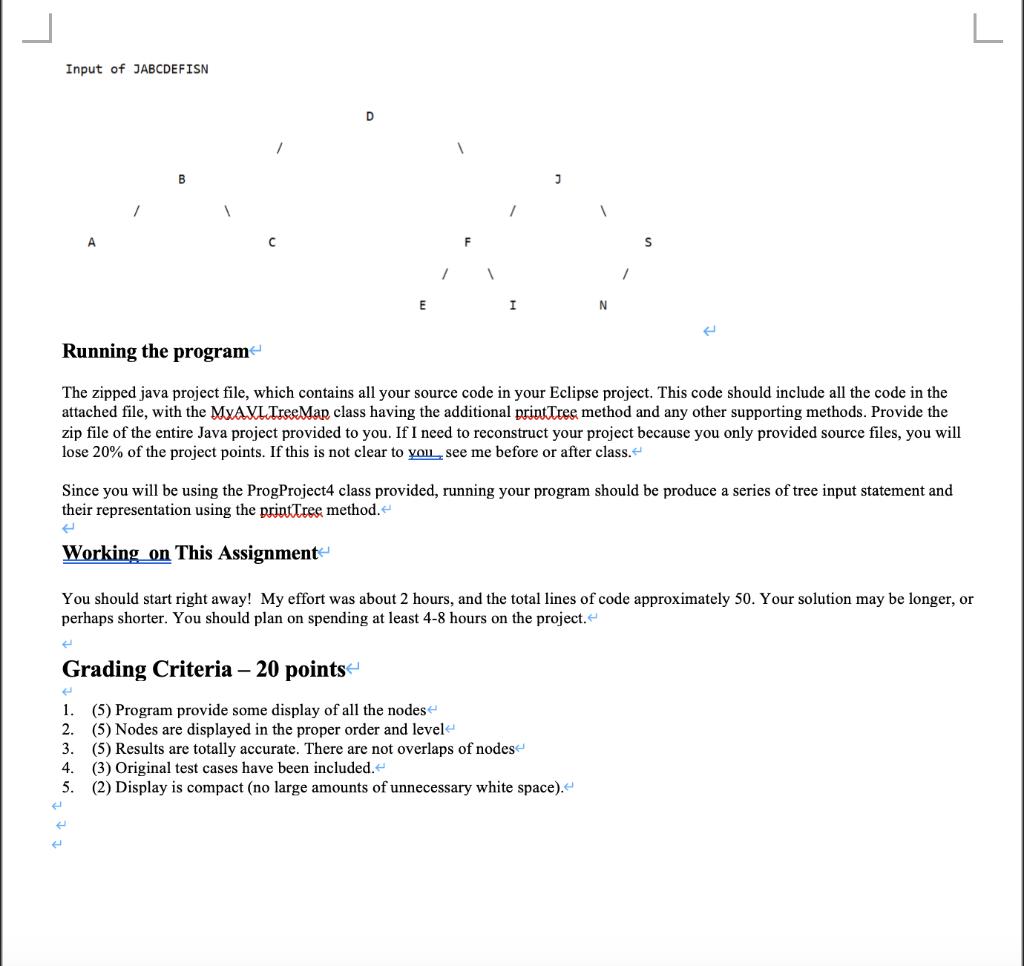
In this project you will populate a Binary Search Tree_(BST), specifically an AVL tree and print out its contents. For example, a tree built from the input: will produce an output similar to the tree below: Input of DACBEFMLGHJK D K. M The goal of the exercise to produce a reasonable facsimile of the tree. Since we are limited by output to the console line, the actual display can not be a perfect graphical representation of the tree. The lines of the trees are not exact but give the symbolic relationships. Objectives The goal of this programming project is for you to master (or at least get practice on) the following tasks: understanding recursion and / or iterative calls within an AVL debugging and checking results Analyzing a problem to determine the best approach working with existing code Start early! This project may not seem like much coding, but debugging always takes time. Analyze and plan now so questions are not being asked a day before the due date. Helpful code: A Main Class and MyAVLTreeMp class have been provided. The main class will use the class provided by the book to build the AVL tree. The example provided builds the 3 trees for you, (though you are requested to include 2 more trees of your own.) that will call methods the AVL class provided. Each element of the tree has a key which is a letter of the input, and value of 1. The value of each element is this project is not relevant.