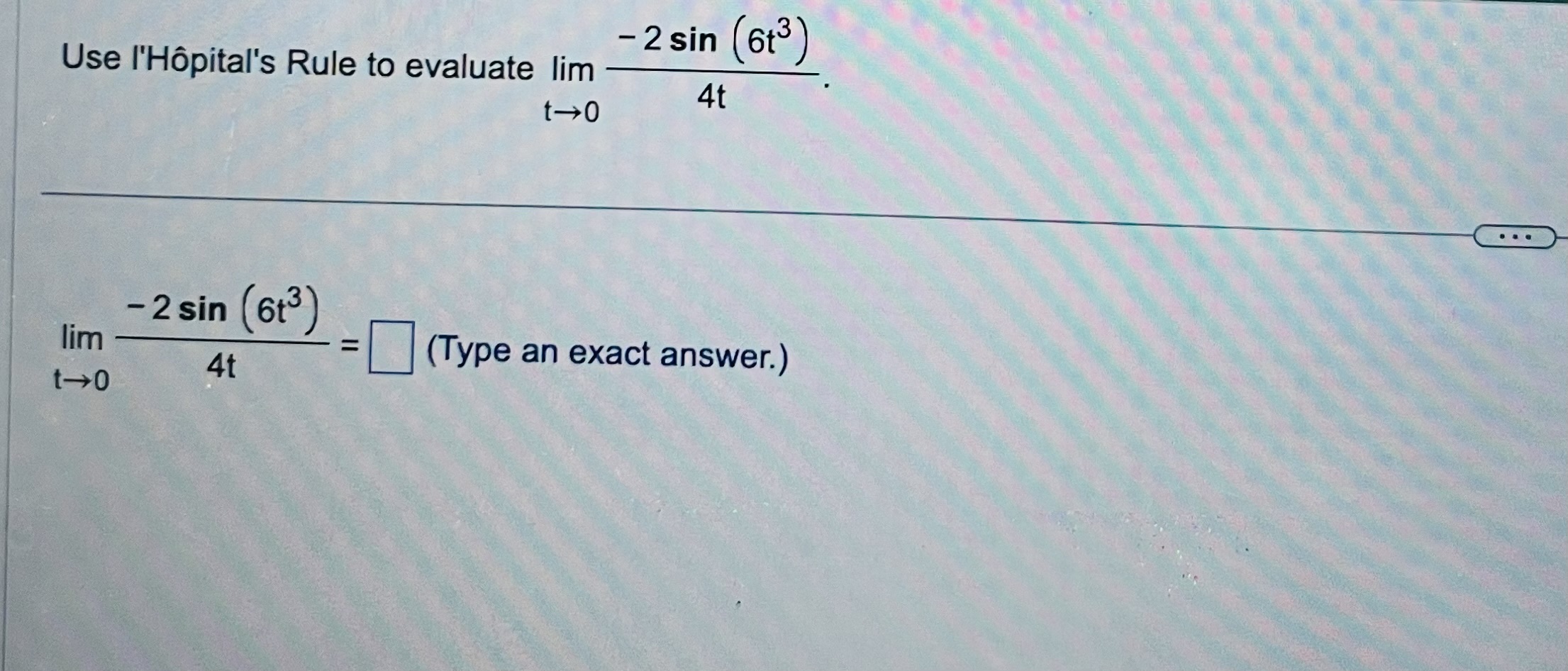
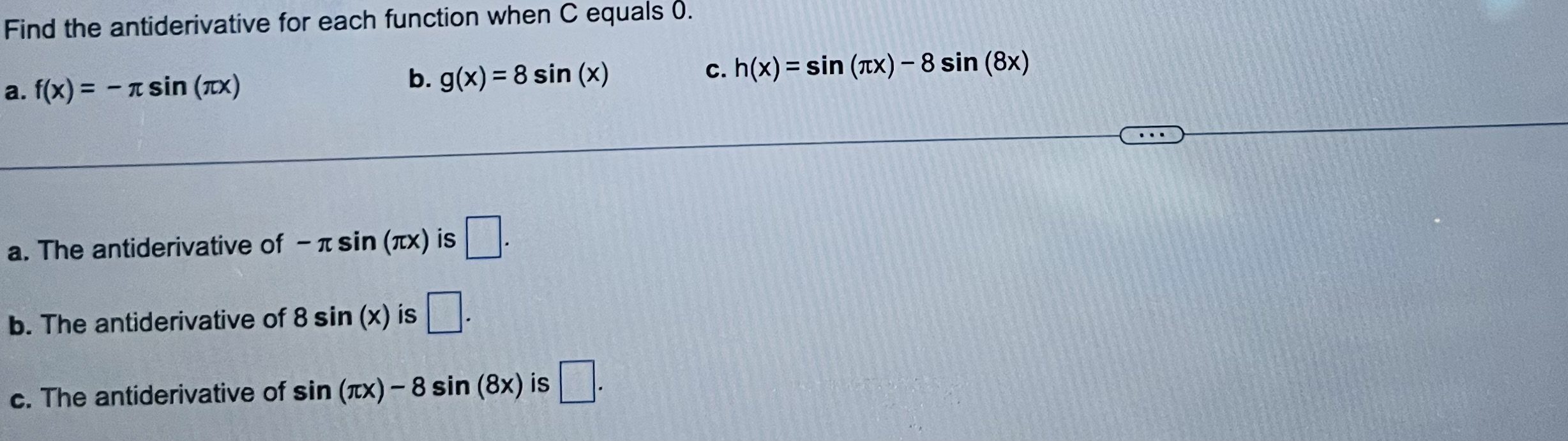
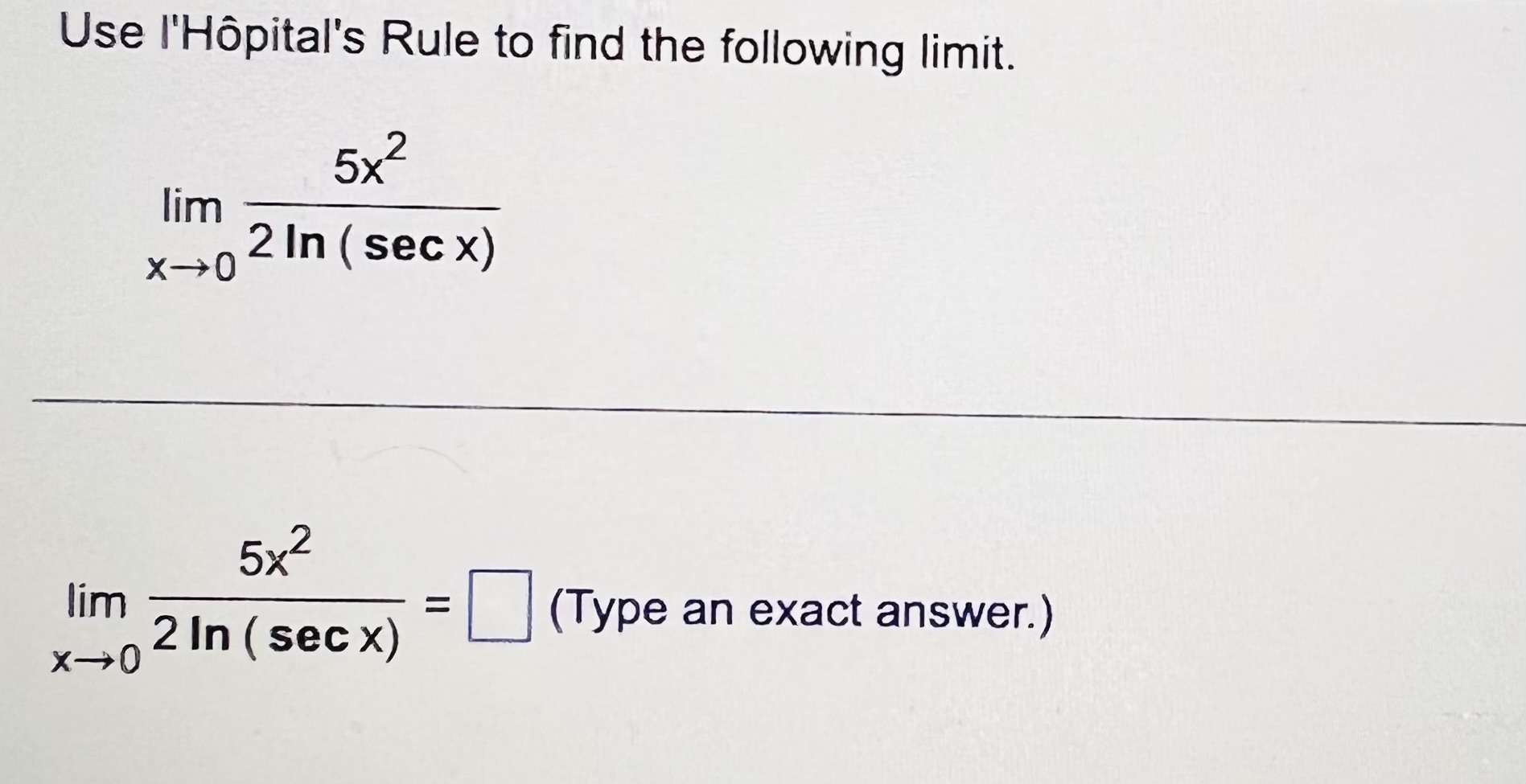In (x + 1) Use I'Hopital's rule to find the limit of lim X-+ 00 log 7 x . . . In (x + 1) lim X -+ 00 log 7 x\fFind the antiderivative for each function when C equals 0. a. f(x) = - n sin (1X) b. g(x) = 8 sin (x) c. h(x) = sin (ntx) - 8 sin (8x) . . . a. The antiderivative of - n sin (1X) is b. The antiderivative of 8 sin (x) is c. The antiderivative of sin (1x) - 8 sin (8x) isds Given the velocity v = and the initial position of a body moving along a coordinate line, find the body's position at time t. V = 9.8t + 2, s(0) = 20 . . . s(t) =A silo (base not included) is to be constructed in the form of a cylinder surmounted by a hemisphere. The cost of construction per square unit of surface area is 6 times as great for the hemisphere as it is for the cylindrical sidewall. Determine the dimensions to be used if the volume is fixed at 12000 cubic units and the cost of construction is to be kept to a minimum. Neglect the thickness of the silo and waste in construction. The radius of the cylindrical base (and of the hemisphere) is ft. (Round to the nearest tenth as needed.) The height of the cylindrical base is |ft. (Round to the nearest tenth.)Use I'Hopital's Rule to find the following limit. 5 x2 lim X -+ 0 2 In ( sec x) 5 x2 lim = 2 In ( sec x) (Type an exact answer.) X-+0