#include #include #include #include using namespace std; // global declation int const null = -1; int const SIZE = 100; int Top = null; // Top of Stack char Q[SIZE], P[SIZE], Stack[SIZE]; // Q is infix and P is postfix expression array int n = 0; // used to count item inserted in P and index for P

void get_Infix ( ) { cout

// following function will do initial work with Q and stack void step_One( ) { strcat(Q,")"); // This function add ) at the and of Q Push('('); // This statement will push first '(' on Stack }

void convert() { while(Top != null ) { for(int i=0;i

} // closing of the convert function void display( ) { P[n]='\0'; // this statement will put string terminator at the // end of P which is Postfix expression cout

} // closing of the convert function void Push(char item) { if(Top == SIZE-1 ){ cout

} char Pop( ) { return Stack[Top--]; }

bool IsEmpty( ) { if(Top == null ) return true; else return false; }

int main() { get_Infix( ); step_One( ); convert( ); display( ); return 0;

} //END OF MAIN FUNCTION

this is the previoes code --------------------------------------------------------------------------------------------

help with code this my code

Transforming Infix Expression into Postfix Expression:

#include #include #include #include using namespace std; // global declation int const null = -1; int const SIZE = 100; int Top = null; // Top of Stack char Q[SIZE], P[SIZE], Stack[SIZE]; // Q is infix and P is postfix expression array int n = 0; // used to count item inserted in P and index for P void display() {

P[n] = '\0'; // this statement will put string terminator at the // end of P which is Postfix expression cout

} // closing of the convert function void Push(char item) {

if (Top == SIZE - 1) { cout

} char Pop() { return Stack[Top--]; }

bool IsEmpty() { if (Top == null) return true; else return false; } void get_Infix ( ) { cout

// following function will do initial work with Q and stack void step_One( ) { strcat(Q,")"); // This function add ) at the and of Q Push('('); // This statement will push first '(' on Stack }

void convert() { while(Top != null ) { for(int i=0;i

} // closing of the convert function

} } } }

int main() {

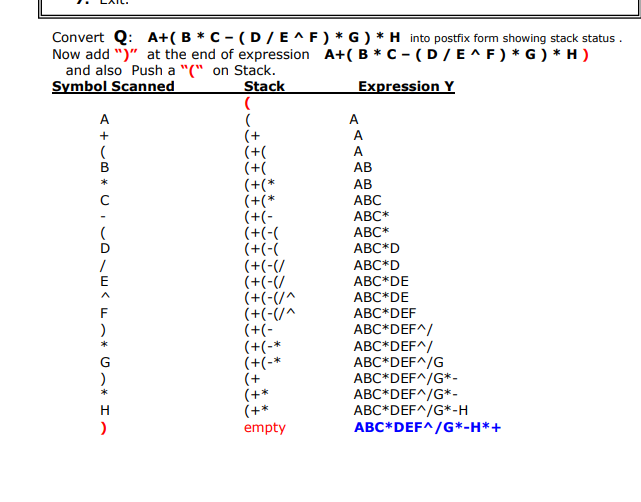
4. Algorithm: Infix_to_PostFix(Q, P) Suppose Q is an arithmetic expression written in infix notation. This algorithm finds the equivalent postfix expression P. 1. Push "C" onto STACK, and add ")" to the end of Q. 2. Scan Q from left to right and repeat Steps 3 to 6 for each element of Q until the STACK is empty: If an operand is encountered, add it to P. If a left parenthesis is encountered, Push it onto STACK. 5. If an operator is encountered, then: a) Repeatedly Pop from STACK and add to P each operator (on the top of STACK) which has the same or higher precedence/priority than b) Push to STACK. [End of If structure.] 6. If a right parenthesis is encountered, then: a) Repeatedly Pop from STACK and add to P each operator (on the top of STACK) until a left parenthesis is encountered. b) Pop the left parenthesis. [Do not add the left parenthesis to P.] [End of If structure.] [End of Step 2 loop.] 7. End. Source code. Transforming Infix Expression into Postfix Expression: The following algorithm transforms the infix expression Q into its equivalent postfix expression P. It uses a stack to temporary hold the operators and left parenthesis. The postfix expression will be constructed from left to right using operands from Q and operators popped from STACK. Algorithm: Infix_to_PostFix(Q, P) Suppose Q is an arithmetic expression written in infix notation. This algorithm finds the equivalent postfix expression P. 1. Push "("onto STACK, and add ")" to the end of Q. 2. Scan Q from left to right and repeat Steps 3 to 6 for each element of Q until the STACK is empty: 3. If an operand is encountered, add it to P. 4. If a left parenthesis is encountered, Push it onto STACK. 5. If an operator is encountered, then: a) Repeatedly Pop from STACK and add to P each operator (on the top of STACK) which has the same or higher precedence/priority than b) Push o to STACK. [End of If structure.] 6. If a right parenthesis is encountered, then: a) Repeatedly Pop from STACK and add to P each operator (on the top of STACK) until a left parenthesis is encountered. b) Pop the left parenthesis. [Do not add the left parenthesis to P.] [End of If structure.] [End of Step 2 loop.] 7. End. Source code: #include #include #include #include // global declation int const null = -1; int const SIZE = 100; int Top = null; // Top of Stack char Q[SIZE], P[SIZE], Stack[SIZE]; // Q is infix and P is postfix expression array int n = 0; // used to count item inserted in P and index for p void get_Infix () { cout mon *+ (+ (+* (+* 4. Algorithm: Infix_to_PostFix(Q, P) Suppose Q is an arithmetic expression written in infix notation. This algorithm finds the equivalent postfix expression P. 1. Push "C" onto STACK, and add ")" to the end of Q. 2. Scan Q from left to right and repeat Steps 3 to 6 for each element of Q until the STACK is empty: If an operand is encountered, add it to P. If a left parenthesis is encountered, Push it onto STACK. 5. If an operator is encountered, then: a) Repeatedly Pop from STACK and add to P each operator (on the top of STACK) which has the same or higher precedence/priority than b) Push to STACK. [End of If structure.] 6. If a right parenthesis is encountered, then: a) Repeatedly Pop from STACK and add to P each operator (on the top of STACK) until a left parenthesis is encountered. b) Pop the left parenthesis. [Do not add the left parenthesis to P.] [End of If structure.] [End of Step 2 loop.] 7. End. Source code. Transforming Infix Expression into Postfix Expression: The following algorithm transforms the infix expression Q into its equivalent postfix expression P. It uses a stack to temporary hold the operators and left parenthesis. The postfix expression will be constructed from left to right using operands from Q and operators popped from STACK. Algorithm: Infix_to_PostFix(Q, P) Suppose Q is an arithmetic expression written in infix notation. This algorithm finds the equivalent postfix expression P. 1. Push "("onto STACK, and add ")" to the end of Q. 2. Scan Q from left to right and repeat Steps 3 to 6 for each element of Q until the STACK is empty: 3. If an operand is encountered, add it to P. 4. If a left parenthesis is encountered, Push it onto STACK. 5. If an operator is encountered, then: a) Repeatedly Pop from STACK and add to P each operator (on the top of STACK) which has the same or higher precedence/priority than b) Push o to STACK. [End of If structure.] 6. If a right parenthesis is encountered, then: a) Repeatedly Pop from STACK and add to P each operator (on the top of STACK) until a left parenthesis is encountered. b) Pop the left parenthesis. [Do not add the left parenthesis to P.] [End of If structure.] [End of Step 2 loop.] 7. End. Source code: #include #include #include #include // global declation int const null = -1; int const SIZE = 100; int Top = null; // Top of Stack char Q[SIZE], P[SIZE], Stack[SIZE]; // Q is infix and P is postfix expression array int n = 0; // used to count item inserted in P and index for p void get_Infix () { cout mon *+ (+ (+* (+*