Inside the dijkstra class method, you are to output the following information to the console screen:

To print out vertex selection sequence

To show the MST nodes by the picked sequence pair with its distance to the starting vertex.

The output shall appears like the following:

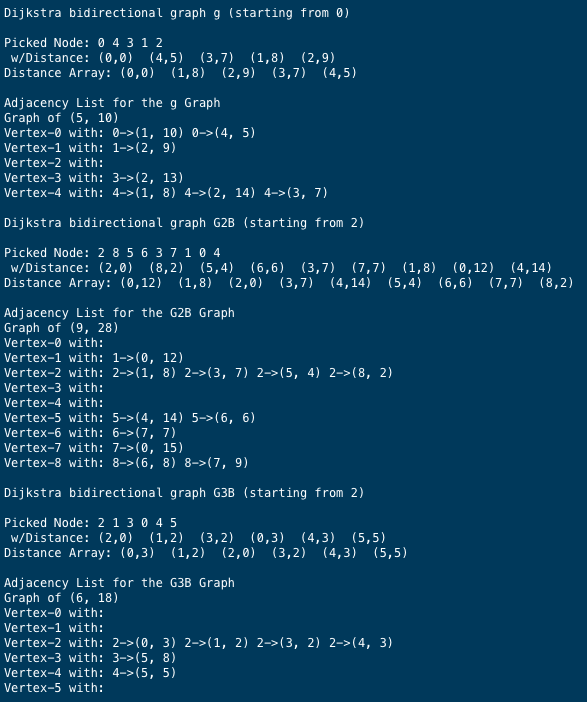
This assignment only expected to complete the edge picking and its proper weight as shown above. The adjacency was illustrated for reference only.

If you have implemented the proper removal of unused edges for the adjacency fix, here is a sample test run on the G4B with some debug trace turned on:

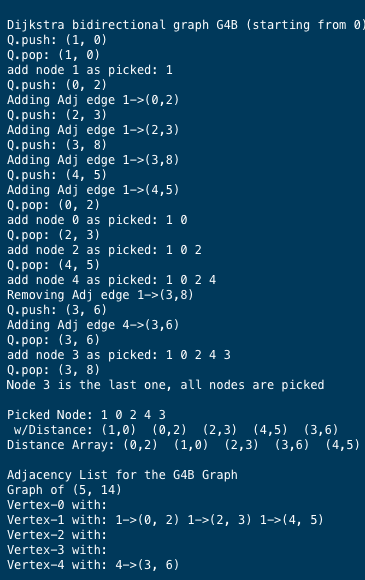
Here's the program that needs to be implemented.

dijkstra.cpp

#include

#include

#include

#include

#include // remove()

#include // INT_MAX

#define ii pair

enum GRAPH_TYPE {DI, BI};

using namespace std;

// functor overloads the compare ii

class compareII {

public:

bool operator()(const ii &j, const ii &k) {

return j.second > k.second;}

};

class Graph

{

int V, E; // No. of vertices, edges

list *adjList; // the djacensy List, alhead pointer to edge list

list *edge; // The edge list from a specific vertex

vector distance; // distances (to starting point) container

vector pv; // picked vertices array

priority_queue, compareII > Q; // type, container, comp

public:

Graph(int v_num) : V(v_num), E(0) {

edge = new list[V];

distance = vector (V, INT_MAX);

}

void addEdge(int u, int v, int w, int type = DI) {

edge[u].push_back(ii(v, w)); E++;

if(type != DI) {

edge[v].push_back(ii(u, w)); E++; }

}

void dijkstra(int v);

void print();

void printGraph();

void printAdjacency();

};

void Graph::printGraph() {

cout

for (auto p : pv) { cout

cout

for (auto p : pv) { cout

cout

for (int n=0; n

cout

cout

}

void Graph::printAdjacency()

{

cout

for (int n = 0; n

cout

for (auto a : adjList[n])

cout ("

cout

}

}

void Graph::dijkstra(int source) {

distance = vector(V, INT_MAX);

distance[source] = 0;

Q.push(ii(source, 0));

adjList = new list[V];

while (!Q.empty()) {

// pop the vertex with smallest distance d of vertex v from Q

// smallest d of v from Q

ii top = Q.top(); Q.pop();

int v = top.first, d = top.second;

// push the selected vertex v into picked vertices array pv

if (d

for (auto e : edge[v]) { // go through all edges e

// if the distance to new node is greater than distance from current node to this node

// replace the distance

// push the new node and distance into the queue

}

}

}

}

// Driver program to test methods of graph class

int main()

{

// Di-graph g(5,10)

Graph g(5);

g.addEdge(0,1,10,DI);

g.addEdge(0,4,5,DI);

g.addEdge(1,2,1,DI);

g.addEdge(1,4,2,DI);

g.addEdge(1,3,4,DI);

g.addEdge(3,0,7,DI);

g.addEdge(3,2,6,DI);

g.addEdge(4,1,3,DI);

g.addEdge(4,2,9,DI);

g.addEdge(4,3,2,DI);

cout

g.dijkstra(0);

g.printGraph();

cout

g.printAdjacency();

// Bidirection G2B (9,28)

Graph G2B(9);

G2B.addEdge(0,1,4,BI);

G2B.addEdge(0,7,8,BI);

G2B.addEdge(1,2,8,BI);

G2B.addEdge(1,7,11,BI);

G2B.addEdge(2,3,7,BI);

G2B.addEdge(2,5,4,BI);

G2B.addEdge(2,8,2,BI);

G2B.addEdge(3,4,9,BI);

G2B.addEdge(3,5,14,BI);

G2B.addEdge(4,5,10,BI);

G2B.addEdge(5,6,2,BI);

G2B.addEdge(6,7,1,BI);

G2B.addEdge(6,8,6,BI);

G2B.addEdge(7,8,7,BI);

cout

G2B.dijkstra(2);

G2B.printGraph();

cout

G2B.printAdjacency();

Graph G3B(6);

G3B.addEdge(0,1,2,BI);

G3B.addEdge(0,2,3,BI);

G3B.addEdge(1,2,2,BI);

G3B.addEdge(1,3,6,BI);

G3B.addEdge(2,3,2,BI);

G3B.addEdge(2,4,3,BI);

G3B.addEdge(3,4,2,BI);

G3B.addEdge(3,5,6,BI);

G3B.addEdge(4,5,2,BI);

cout

G3B.dijkstra(2);

G3B.printGraph();

cout

G3B.printAdjacency();

// 2 3

// (0)--(1)--(2)

// | / \ |

// 6| 8/ \5 |4

// | / 1 \ |

// (3)-------(4)

Graph G4B(5);

G4B.addEdge(0,1,2,BI);

G4B.addEdge(0,3,6,BI);

G4B.addEdge(1,2,3,BI);

G4B.addEdge(1,3,8,BI);

G4B.addEdge(1,4,5,BI);

G4B.addEdge(2,4,4,BI);

G4B.addEdge(3,4,1,BI);

cout

G4B.dijkstra(1);

G4B.printGraph();

cout

G4B.printAdjacency();

return 0;

Dijkstra bidirectional graph g (starting from 0) Picked Node: 0 4 31 2 w/Distance: (0,0) (4,5) (3,7) (1,8) (2,9) Distance Array: (0,0) (1,8) (2,9) (3,7) (4,5) Adjacency List for the g Graph Graph of (5, 10) Vertex-0 with: 0-(1, 10) 0->(4, 5) Vertex-1 with: 1->(2, 9) Vertex-2 with: Vertex-3 with: 3->(2, 13) Vertex-4 with: 4->(1, 8) 4-(2, 14) 4->(3, 7) Dijkstra bidirectional graph G2B (starting from 2) Picked Node: 28 56 3710 4 w/Distance: (2,0) (8,2) (5,4) (6,6) (3,7) (7,7) (1,8) (0,12) (4,14) Distance Array: (0,12) (1,8) (2,0) (3,7) (4,14) (5,4) (6,6) (7,7) (8,2) Adjacency List for the G2B Graph Graph of (9, 28) Vertex-0 with: Vertex-1 with: 1->(0, 12) Vertex-2 with: 2->(1, 8) 2-(3, 7) 2->(5, 4) 2->(8, 2) Vertex-3 with: Vertex-4 with Vertex-5 with: 5->(4, 14) 5->(6, 6) Vertex-6 with: 6->(7, 7) Vertex-7 with: 7->(0, 15) Vertex-8 with: 8->(6, 8) 8-(7, 9) Dijkstra bidirectional graph G3B (starting from 2) Picked Node: 2 130 4 5 w/Distance: (2,0) (1,2) (3,2) (0,3) (4,3) (5,5) Distance Array: (0,3) (1,2) (2,0) (3,2) (4,3) (5,5) Adjacency List for the G3B Graph Graph of (6, 18) Vertex-0 with: Vertex-1 with: Vertex-2 with: 2->(0, 3) 2-(1, 2) 2->(3, 2) 2->(4, 3) Vertex-3 with: 3->(5, 8) Vertex-4 with: 4->(5, 5) Vertex-5 with: Dijkstra bidirectional graph g (starting from 0) Picked Node: 0 4 31 2 w/Distance: (0,0) (4,5) (3,7) (1,8) (2,9) Distance Array: (0,0) (1,8) (2,9) (3,7) (4,5) Adjacency List for the g Graph Graph of (5, 10) Vertex-0 with: 0-(1, 10) 0->(4, 5) Vertex-1 with: 1->(2, 9) Vertex-2 with: Vertex-3 with: 3->(2, 13) Vertex-4 with: 4->(1, 8) 4-(2, 14) 4->(3, 7) Dijkstra bidirectional graph G2B (starting from 2) Picked Node: 28 56 3710 4 w/Distance: (2,0) (8,2) (5,4) (6,6) (3,7) (7,7) (1,8) (0,12) (4,14) Distance Array: (0,12) (1,8) (2,0) (3,7) (4,14) (5,4) (6,6) (7,7) (8,2) Adjacency List for the G2B Graph Graph of (9, 28) Vertex-0 with: Vertex-1 with: 1->(0, 12) Vertex-2 with: 2->(1, 8) 2-(3, 7) 2->(5, 4) 2->(8, 2) Vertex-3 with: Vertex-4 with Vertex-5 with: 5->(4, 14) 5->(6, 6) Vertex-6 with: 6->(7, 7) Vertex-7 with: 7->(0, 15) Vertex-8 with: 8->(6, 8) 8-(7, 9) Dijkstra bidirectional graph G3B (starting from 2) Picked Node: 2 130 4 5 w/Distance: (2,0) (1,2) (3,2) (0,3) (4,3) (5,5) Distance Array: (0,3) (1,2) (2,0) (3,2) (4,3) (5,5) Adjacency List for the G3B Graph Graph of (6, 18) Vertex-0 with: Vertex-1 with: Vertex-2 with: 2->(0, 3) 2-(1, 2) 2->(3, 2) 2->(4, 3) Vertex-3 with: 3->(5, 8) Vertex-4 with: 4->(5, 5) Vertex-5 with