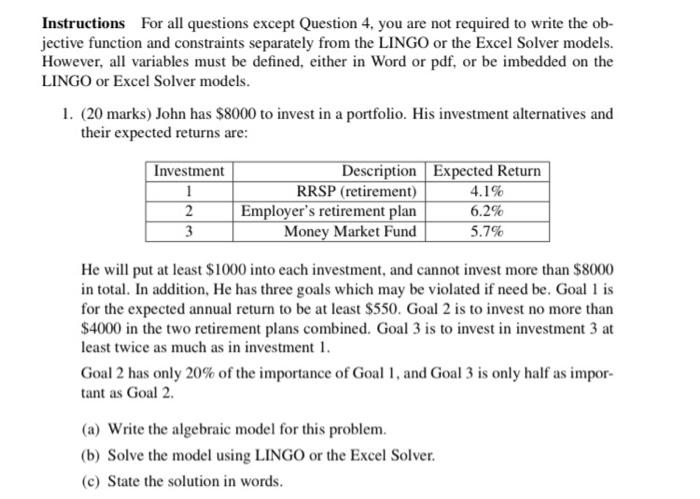
Instructions For all questions except Question 4, you are not required to write the ob- jective function and constraints separately from the LINGO or the Excel Solver models. However, all variables must be defined, either in Word or pdf, or be imbedded on the LINGO or Excel Solver models. 1. (20 marks) John has $8000 to invest in a portfolio. His investment alternatives and their expected returns are: Investment 1 2 3 Description Expected Return RRSP (retirement) 4.1% Employer's retirement plan 6.2% Money Market Fund 5.7% He will put at least $1000 into each investment, and cannot invest more than $8000 in total. In addition, He has three goals which may be violated if need be. Goal 1 is for the expected annual return to be at least $550. Goal 2 is to invest no more than $4000 in the two retirement plans combined. Goal 3 is to invest in investment 3 at least twice as much as in investment 1. Goal 2 has only 20% of the importance of Goal 1, and Goal 3 is only half as impor- tant as Goal 2. (a) Write the algebraic model for this problem. (b) Solve the model using LINGO or the Excel Solver. (c) State the solution in words. Instructions For all questions except Question 4, you are not required to write the ob- jective function and constraints separately from the LINGO or the Excel Solver models. However, all variables must be defined, either in Word or pdf, or be imbedded on the LINGO or Excel Solver models. 1. (20 marks) John has $8000 to invest in a portfolio. His investment alternatives and their expected returns are: Investment 1 2 3 Description Expected Return RRSP (retirement) 4.1% Employer's retirement plan 6.2% Money Market Fund 5.7% He will put at least $1000 into each investment, and cannot invest more than $8000 in total. In addition, He has three goals which may be violated if need be. Goal 1 is for the expected annual return to be at least $550. Goal 2 is to invest no more than $4000 in the two retirement plans combined. Goal 3 is to invest in investment 3 at least twice as much as in investment 1. Goal 2 has only 20% of the importance of Goal 1, and Goal 3 is only half as impor- tant as Goal 2. (a) Write the algebraic model for this problem. (b) Solve the model using LINGO or the Excel Solver. (c) State the solution in words