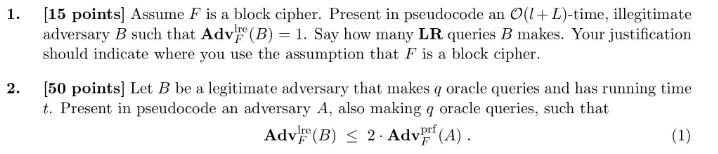
Instructions: Justifications and explanations for answers are always required, and answers without them may not get credit. See course information sheet for rules, and information about quality of exposition. We adopt the convention that the running time of an adversary excludes the time taken by game procedures. So, a call to a game procedure takes time O(n + m) where n. m are the lengths of the procedure inputs and outputs, respectively. Problem 1 [100 points] Let F: {0,1} {0,1} {0,1} be a family of functions, where 1, L2 128. Consider the following game: For an adversary B, let Game LREF procedure Initialize K (0,1); b {0,1} procedure LR(20, 1) // 0,1 {0,1}' Ret F(K, b) procedure Finalize(b') Ret (b= b) Adv (B) = 2. Pr [LRE true] - 1. Let (x,x),(a, a) be the queries that B makes to its oracle. (Each query is a pair of l-bit strings, and there are q queries in all.) We say that B is legitimate if ..... are all distinct, and also x,..., are all distinct. We say that F is LRE-secure if Adv (B) is "small" for every legitimate B of "practical" resources. Ire 1. [15 points] Assume F is a block cipher. Present in pseudocode an O(l+L)-time, illegitimate adversary B such that Adv (B) = 1. Say how many LR queries B makes. Your justification should indicate where you use the assumption that F is a block cipher. 2. [50 points] Let B be a legitimate adversary that makes q oracle queries and has running time t. Present in pseudocode an adversary A, also making q oracle queries, such that Adv (B) 2. Adv (A). F (1) 3. 4. The running time of A, which you should state, should be close to t, and you should prove that Eq. (1) holds. [5 points] Explain why (2.) shows that if F is a secure PRF then it is LRE-secure. [30 points] Is the converse true? Namely, if F is LRE-secure, then is it a secure PRF? Answer YES or NO. If you say YES, justify this via a reduction-based proof, and, if NO, via a counterexample. (The latter means a particular family of functions F which you prove is LRE-secure but which you show via an attack is not PRF-secure.)