international trade

melitz model

firm heteogous

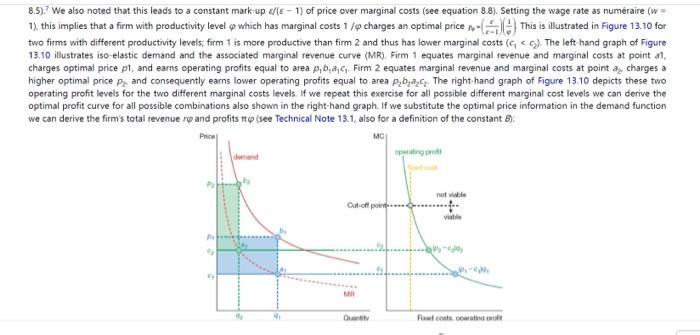
QUESTION 13-3 (TECHNICAL) Suppose the economic conditions in Mirandia are perfectly described by the Melitz model of sections 13.4 to 13.6 and the ex ante productivity distribution function is umiform from 0 to 5 . Moreover, assume that in autarky only 80 per cent of the entrepreneurs who invest in setting up a new firm actually succeed. a. What is the autarky cut-off productivity level? b. What is the ex ante average productivity? What is the ex post average productivity in autarky? The government of Mirandia opens up international trade possibilities with Marconia. As a consequence, only 60 per cent of the entrepreneurs who invest in setting up a new firm actually succeed. Of the viable firms only one-third become exporters. c. What is the trade cut-off productivity level? d. What is the export cut-off productivity level? e. What is the ex post average productivity with trade? f. What is the average productivity for exporting firms? g. What do you consider the best indicator of the new source of gains from trade explained in this chapter using (a combination of) your answers to the questions above? Building on Hopenhayn's (1992a, 1992b) work on endogenous selection of heterogeneous firms in a sector and Krugman's (1979, 1980) model of trade under monopolistic competition with increasing returns to scale, Melitz (2003) develops an ingenious dynamic model in which (i) less productive firms exit the market, (ii) intermediately productive firms produce only for the local market, and (iii) the most productive firms both export and produce for the local market. The Melitz approach is based on the monopolistic competition model of intra-industry trade discussed in Chapter 8 with one important difference: instead of all firms having identical technology, a firm may now be identified by its productivity level (which differs among firms). As in Chapter 8 there is increasing returns to seale at the firm level due to a (per period) foced cost t, which we assume to be the same for all firms. Firm productivity heterogeneity arises from differences in marginal production costs. More specifically, for a firm with productivity level the labour costs involved in producing qunits of a good are f+q/. As we will see, firms with different productivity levels charge different prices, produce different quantities, and so on. We denote these variables with a sub-index . The main structure of the model is illustrated in Figure 13.9. There is a large number M of active firms in the economy, each producing a differentiated good under monopolistic competition. Since the firms differ in their productivity levels . they have different levels of operating profits. 6 Firm exit at this stage occurs with an exogenous probability of bad luck , identical for all firms. In each period M active firms therefore exit the market. The prospective of earning positive operating profits entices Men firms, out of an unlimited pool of potential entrants, to try to enter the market. Each of these firms incurs a fixed entry cost fe1 for their attempt (note that these entry costs differ from the per-period foxed costs f. In equilibrium. the total entry costs fenMen are equal to the total operating profits. The only uncertainty in the model involves the ex ante firm productivity level, which is resolved upon investing the one-time entry costs. Once the firm productivity level is known, the entrepreneur can determine if it is possible to eam positive operating profits. If not - that is, if the productivity level is below a certain threshold p. - the potential entrant will immediately exit the market with probability G(1). The remaining 1 - G. p1) firms do in fact enter the market succesfully. In the stationary equilibrium, the number of entrants is equal to the number of active firms that exit the market M and the total number of active firms does not change. 8.5)7 We also noted that this leads to a constant mark-up /(1) of price over marginal costs (see equation 8.8 ). Setting the wage rate as numraire ( w= 1), this implies that a firm with productivity level which has marginal costs 1/ charges an optimal price =(c1c)(1) This is illustrated in Figure 13.10 for two tirms with different productivity levels, firm 1 is more productive than firm 2 and thus has lower marginal costs ( c1 p.l. the firm makes a positive operating protit each period it survives in the market. Per period the operating profit is (821. see equation 13.1. Since the probability of exit in any period is equal to the probability that the firm is still operative after t periods is (1 - 8)t. Ignoring discounting for simplicity, the net present value of the operating profits is therefore equal to (81f)/a If this value is less than the entry costs ten the entrant will still make an ex post loss; only if this value is larger than the entry costs will the entrant make an ex post expected profit. The probability of any particular outcome occurring is, of course, given by the pdf g(). The free entry condition for potential entrants ensures that the ex ante expected value of discounted profits is equal to the entry costs ftid QUESTION 13-3 (TECHNICAL) Suppose the economic conditions in Mirandia are perfectly described by the Melitz model of sections 13.4 to 13.6 and the ex ante productivity distribution function is umiform from 0 to 5 . Moreover, assume that in autarky only 80 per cent of the entrepreneurs who invest in setting up a new firm actually succeed. a. What is the autarky cut-off productivity level? b. What is the ex ante average productivity? What is the ex post average productivity in autarky? The government of Mirandia opens up international trade possibilities with Marconia. As a consequence, only 60 per cent of the entrepreneurs who invest in setting up a new firm actually succeed. Of the viable firms only one-third become exporters. c. What is the trade cut-off productivity level? d. What is the export cut-off productivity level? e. What is the ex post average productivity with trade? f. What is the average productivity for exporting firms? g. What do you consider the best indicator of the new source of gains from trade explained in this chapter using (a combination of) your answers to the questions above? Building on Hopenhayn's (1992a, 1992b) work on endogenous selection of heterogeneous firms in a sector and Krugman's (1979, 1980) model of trade under monopolistic competition with increasing returns to scale, Melitz (2003) develops an ingenious dynamic model in which (i) less productive firms exit the market, (ii) intermediately productive firms produce only for the local market, and (iii) the most productive firms both export and produce for the local market. The Melitz approach is based on the monopolistic competition model of intra-industry trade discussed in Chapter 8 with one important difference: instead of all firms having identical technology, a firm may now be identified by its productivity level (which differs among firms). As in Chapter 8 there is increasing returns to seale at the firm level due to a (per period) foced cost t, which we assume to be the same for all firms. Firm productivity heterogeneity arises from differences in marginal production costs. More specifically, for a firm with productivity level the labour costs involved in producing qunits of a good are f+q/. As we will see, firms with different productivity levels charge different prices, produce different quantities, and so on. We denote these variables with a sub-index . The main structure of the model is illustrated in Figure 13.9. There is a large number M of active firms in the economy, each producing a differentiated good under monopolistic competition. Since the firms differ in their productivity levels . they have different levels of operating profits. 6 Firm exit at this stage occurs with an exogenous probability of bad luck , identical for all firms. In each period M active firms therefore exit the market. The prospective of earning positive operating profits entices Men firms, out of an unlimited pool of potential entrants, to try to enter the market. Each of these firms incurs a fixed entry cost fe1 for their attempt (note that these entry costs differ from the per-period foxed costs f. In equilibrium. the total entry costs fenMen are equal to the total operating profits. The only uncertainty in the model involves the ex ante firm productivity level, which is resolved upon investing the one-time entry costs. Once the firm productivity level is known, the entrepreneur can determine if it is possible to eam positive operating profits. If not - that is, if the productivity level is below a certain threshold p. - the potential entrant will immediately exit the market with probability G(1). The remaining 1 - G. p1) firms do in fact enter the market succesfully. In the stationary equilibrium, the number of entrants is equal to the number of active firms that exit the market M and the total number of active firms does not change. 8.5)7 We also noted that this leads to a constant mark-up /(1) of price over marginal costs (see equation 8.8 ). Setting the wage rate as numraire ( w= 1), this implies that a firm with productivity level which has marginal costs 1/ charges an optimal price =(c1c)(1) This is illustrated in Figure 13.10 for two tirms with different productivity levels, firm 1 is more productive than firm 2 and thus has lower marginal costs ( c1 p.l. the firm makes a positive operating protit each period it survives in the market. Per period the operating profit is (821. see equation 13.1. Since the probability of exit in any period is equal to the probability that the firm is still operative after t periods is (1 - 8)t. Ignoring discounting for simplicity, the net present value of the operating profits is therefore equal to (81f)/a If this value is less than the entry costs ten the entrant will still make an ex post loss; only if this value is larger than the entry costs will the entrant make an ex post expected profit. The probability of any particular outcome occurring is, of course, given by the pdf g(). The free entry condition for potential entrants ensures that the ex ante expected value of discounted profits is equal to the entry costs ftid