Intro to Java *30.18 (Parallel Eight Queens) Revise Listing 22.11, EightQueens.java, to develop a parallel algorithm that finds all solutions for the Eight Queens problem.

(Hint: Launch eight subtasks, each of which places the queen in a different column in the first row.)

below is the Listing 22.11

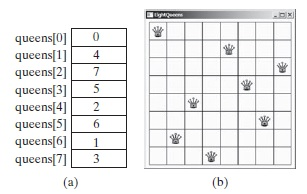
/**To see how the algorithm works, go to www.cs.armstrong.edu/liang/animation/EightQueensAnimation.html. Listing 22.11 gives the program that displays a solution for the Eight Queens problem. 22.9 Solving the Eight Queens Problem Using Backtracking page 847 This section solves the Eight Queens problem using the backtracking approach. The Eight Queens problem is to find a solution to place a queen in each row on a chessboard such that no two queens can attack each other. The problem can be solved using recursion (See Programming Exercise 18.34). In this section, we will introduce a common algorithm design technique called backtracking for solving this problem. The backtracking approach searches for a candidate solution incrementally, abandoning that option as soon as it determines that the candidate cannot possibly be a valid solution, and then looks for a new candidate. You can use a two-dimensional array to represent a chessboard. However, since each row can have only one queen, it is sufficient to use a one-dimensional array to denote the position of the queen in the row. Thus, you can define the queens array as: int[] queens = new int[8]; Assign j to queens[i] to denote that a queen is placed in row i and column j. Figure 22.6a shows the contents of the queens array for the chessboard in Figure 22.6b. LISTING 22.11 EightQueens.java */ import javafx.application.Application; import javafx.geometry.Pos; import javafx.stage.Stage; import javafx.scene.Scene; import javafx.scene.control.Label; import javafx.scene.image.Image; import javafx.scene.image.ImageView; import javafx.scene.layout.GridPane; public class EightQueens extends Application { public static final int SIZE = 8; // The size of the chess board // queens are placed at (i, queens[i]) // -1 indicates that no queen is currently placed in the ith row // Initially, place a queen at (0, 0) in the 0th row private int[] queens = {-1, -1, -1, -1, -1, -1, -1, -1}; @Override // Override the start method in the Application class public void start(Stage primaryStage) { search(); // Search for a solution // Display chess board GridPane chessBoard = new GridPane(); chessBoard.setAlignment(Pos.CENTER); Label[][] labels = new Label[SIZE][SIZE]; for (int i = 0; i = 0 && k

The program invokes search() (line 19) to search for a solution. Initially, no queens are

placed in any rows (line 15). The search now starts from the first row with k = 0 (line 48) and

finds a place for the queen (line 51). If successful, place it in the row (line 56) and consider the

next row (line 57). If not successful, backtrack to the previous row (lines 5354).

The findPosition(k) method searches for a possible position to place a queen in row

k starting from queen[k] + 1 (line 68). It checks whether a queen can be placed at start,

start + 1, . . . , and 7, in this order (lines 7073). If possible, return the column index

(line 72); otherwise, return -1 (line 75).

The isValid(row, column) method is called to check whether placing a queen at the

specified position causes a conflict with the queens placed earlier (line 71). It ensures that no

queen is placed in the same column (line 81), in the upper-left diagonal (line 82), or in the

upper-right diagonal (line 83), as shown in Figure 22.7.

queens queens queens queens queens [4] 2 queens 6 queens 1 queens 3 (a) (b) queens queens queens queens queens [4] 2 queens 6 queens 1 queens 3 (a) (b)