Introduction:

It is recommended that students shall finish learning chapter 5: Finite Automata before working on the following homework.

In CS 4110, many discussed machines, including Finite Automata and Pushdown Automata, are finite-state machines (FSM). A FSM is an abstract machine that can be in exactly one of a finite number of states at any given moment. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition.

The behavior of state machines can be observed in many devices in modern society that perform a predetermined sequence of actions depending on a sequence of events with which they are presented. Simple examples are vending machines, which dispense products when the proper combination of coins is deposited; elevators, whose sequence of stops is determined by the floors requested by riders; traffic lights, which change sequence when cars are waiting; and combination locks, which require the input of a sequence of numbers in the proper order.

Example:

Consider the model of a simple vending machine. The machine is initially in the "ready" state, which maps to exactly two states in the following way:

• ready -> deposit -> waiting
• ready -> quit -> exit

The variables in bold-face represent transitions. Any input signal not corresponding to one of those transitions can either trigger an error or be ignored. Otherwise, the current state is updated and the process is repeated. If, for example, a deposit input signal is encountered, the FSM will move to the "waiting" state, which defines these transitions:

• waiting -> select -> dispense
• waiting -> refund -> refunding

The "dispense" state defines only one transition:

• dispense -> remove -> ready

Note, however, that in this example the "refunding" state doesn't actually require input in order to move to the "ready" state, so an implicit transition is defined as such:

• refunding -> ready

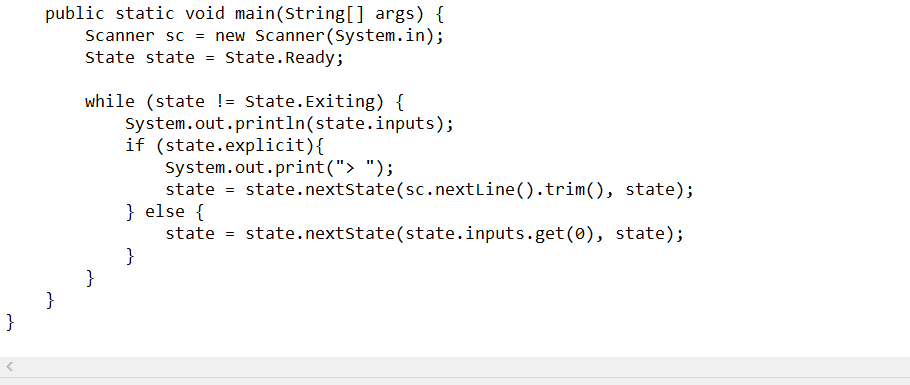
A sample Java program is provided to implement a finite state machine which handles both explicit and implicit transitions. Your are required to finish the following tasks for this

homework:

• Task 1 (5 points): in the above given example, we need to modify the "refunding" state transition such that it requires the refunded money to be removed in order to move to the "ready" state, so the modified transition is defined as such: refunding -> remove -> ready. You are required to modify the given Java program to implement the updated transition.
• 
• 

import java.util.*; public class VendingMachine { private enum state { Ready(true, "Deposit", "Quit"), Waiting(true, "Select", "Refund"), Dispensing(true,"Remove"), Refunding(false, "Refunding"), Exiting(false, "Quiting"); state(boolean exp, string... in) { inputs = Arrays.aslist(in); explicit = exp; } state nextstate(String input, state current) { if (inputs.contains(input)) { return map.getOrDefault(input, current); } return current; } final List inputs; final static Map map = new HashMap(); final boolean explicit; static { map.put("Deposit", state.Waiting); map.put("Quit", state. Exiting); map.put("select", State.Dispensing); map.put("Refund", State. Refunding); map.put("Remove", state. Ready); map.put("Refunding", state. Ready); } } public static void main(String[] args) { Scanner sc = new Scanner(System.in); State state state. Ready; while (state != State. Exiting) { System.out.println(state. inputs); if (state.explicit){ System.out.print(" "); state = state.nextstate(sc.nextLine().trim(), state); } else { state = state.nextstate(state. inputs.get(0), state); } } } } import java.util.*; public class VendingMachine { private enum state { Ready(true, "Deposit", "Quit"), Waiting(true, "Select", "Refund"), Dispensing(true,"Remove"), Refunding(false, "Refunding"), Exiting(false, "Quiting"); state(boolean exp, string... in) { inputs = Arrays.aslist(in); explicit = exp; } state nextstate(String input, state current) { if (inputs.contains(input)) { return map.getOrDefault(input, current); } return current; } final List inputs; final static Map map = new HashMap(); final boolean explicit; static { map.put("Deposit", state.Waiting); map.put("Quit", state. Exiting); map.put("select", State.Dispensing); map.put("Refund", State. Refunding); map.put("Remove", state. Ready); map.put("Refunding", state. Ready); } } public static void main(String[] args) { Scanner sc = new Scanner(System.in); State state state. Ready; while (state != State. Exiting) { System.out.println(state. inputs); if (state.explicit){ System.out.print(" "); state = state.nextstate(sc.nextLine().trim(), state); } else { state = state.nextstate(state. inputs.get(0), state); } } } }