Introduction to LabVIEW H&W (do the No. 2 question)

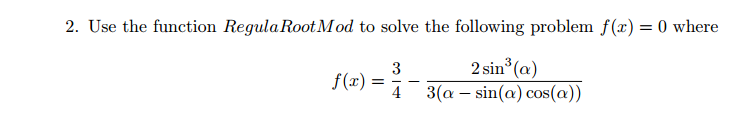
function ModRegFal = ModRegFal(a, b, n) 

format long; 

a = input('Enter a value for lower boundary a: '); b = input('Enter a value for upper boundary b: '); n = input('How small should should the error be (to what -power)? '); 

if (f(a)*f(b) > 0 ) disp ('Invalid values of a and b. Program Closing') return; end; 

F = f(a); G = f(b); w0 = a; 

while (1) wn = (G*a-F*b)/(G-F); disp([a b wn w0]) %% just checking where the values are, and it they look correct if f(a)*f(wn) > 0 disp('ranif 1')%% just checking where the values are, and it they look correct b = wn; G = f(wn); if f(w0)*f(wn) > 0 F = F/ 2; end; disp('ranif 2')%% just checking where the values are, and it they look correct disp([a b wn w0])%% just checking where the values are, and it they look correct else a = wn; F = f(wn); if f(w0)*f(wn) > 0 disp('ranif 3')%% just checking where the values are, and it they look correct disp([a b wn w0])%% just checking where the values are, and it they look correct G = G/ 2; end; end disp([a b wn w0]) if (abs((wn - w0)/wn)  
plot (error)
 
grid on;
 
title('Plot of error');
 
xlabel('iterations');
 
ylabel('Error');
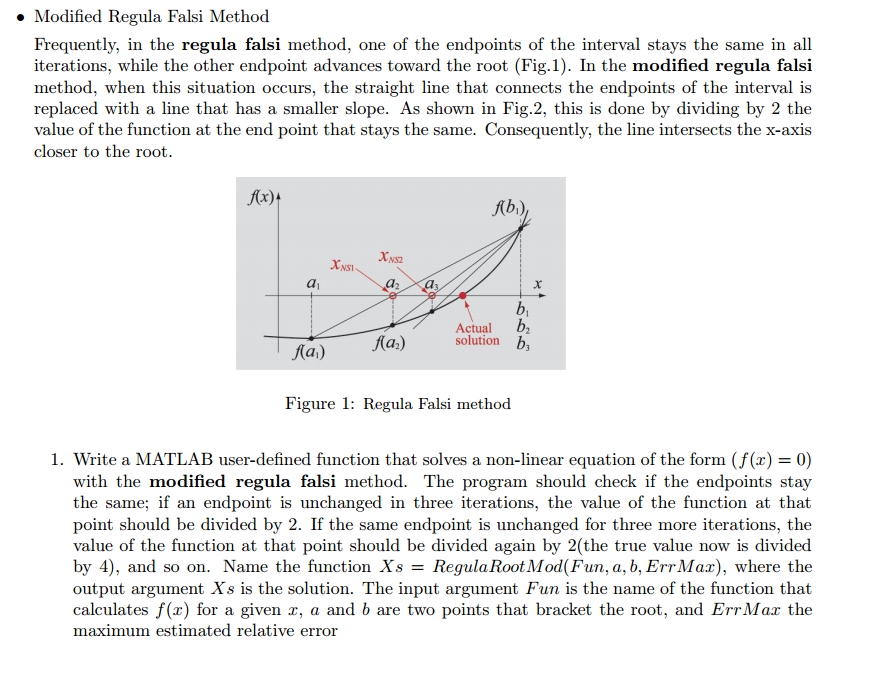
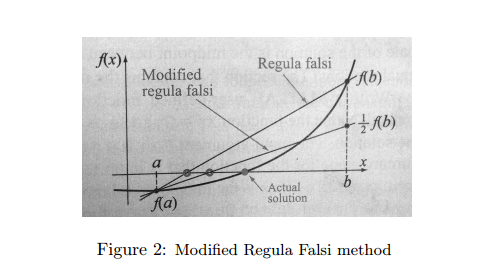
   Modified Regula Falsi Method Frequently, in the regula falsi method, one of the endpoints of the interval stays the same in all iterations, while the other endpoint advances toward the root (Fig.1). In the modified regula falsi method, when this situation occurs, the straight line that connects the endpoints of the interval is replaced with a line that has a smaller slope. As shown in Fig.2, this is done by dividing by 2 the value of the function at the end point that stays the same. Consequently, the line intersects the x-axis closer to the root f(x)t Abi) NS2 NSI ActualD2 solution Ka) Figure 1: Regula Falsi method I. Write a MATLAB user-defined function that solves a non-linear equation of the form (f(x) = 0) with the modified regula falsi method. The program should check if the endpoints stay the same; if an endpoint is unchanged in three iterations, the value of the function at that point should be divided by 2. If the same endpoint is unchanged for three more iterations, the value of the function at that point should be divided again by 2(the true value now is divided by 4), and so on. Name the function Xs = RegulaRootMod(Fun, a, b, ErrMax), where the output argument Xs is the solution. The input argument Fun is the name of the function that calculates f(x) for a given r, a and b are two points that bracket the root, and ErrMar the maximum estimated relative error