1. Introduction to the Prim Algorithm for MST

(1) The definition of Minimum spanning trees (MST):

• G = (V, E) is a weighted connected undirected graph;
• Spanning tree is S = (V, T), T E, undirected tree;
• Minimum spanning tree (MST) is a spanning tree with the smallest total weight.

(2) The Prim Algorithm for finding MST:

Step 1: x V, Let A = {x}, B = V - {x}.

Step 2: Select (u, v) E, u A, v B such that (u, v) has the smallest weight between A and B.

Step 3: Put (u, v) in the tree. A = A {v}, B = B - {v}

Step 4: If B = , stop; otherwise, go to Step 2.

2. Experimental Purpose

(1)Understand what is the Minimum spanning trees (MST);

(2)Learn what kinds of algorithms can be used to find MST, such as: Kruskal and Prim algorithms;

(3)Compare the difference between these two algorithms;

3. Experimental Contents

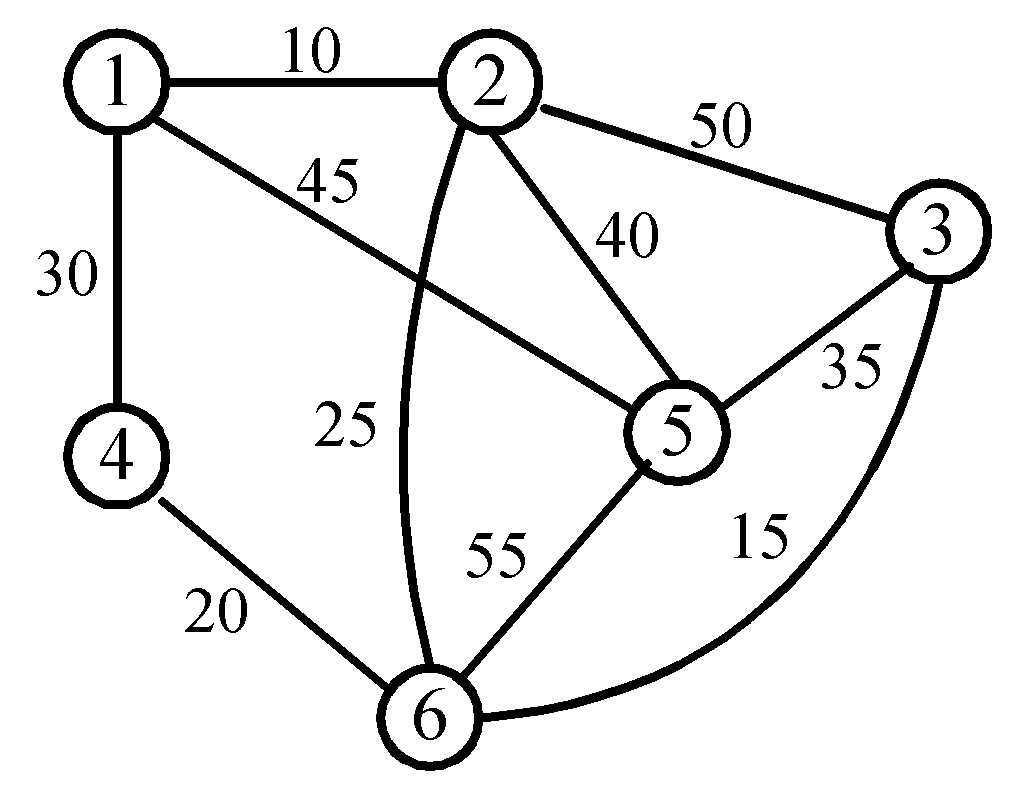
(1) Given a undirected Graph G=(V, E) like below, to calculate the minimum spanning tree using Kruskals algorithm and Prims algorithm.

4. Experimental Requirement

1. The template should be used for all kinds of data type, such as: integer, real, double, etc. in the program;
2. Programs should be made by Object-Oriented Programming (OOP) method;
3. Use using Kruskals algorithm and Prims algorithm to solve this problem.
4. And compare the results between these two algorithms and the difference of selection processes.
5. Write down the report in which there should be the execution results of the program.

10 50 45 40 3 30 35 25 4 5 55 15 20