IT SHOULD BE DONE IN PYTHON. THANK YOU

BELOW IS AN EXAMPLE AND SOLUTION

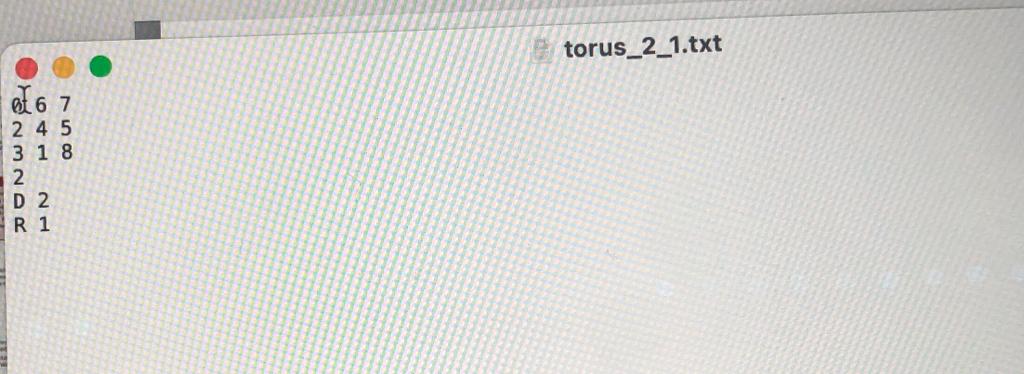
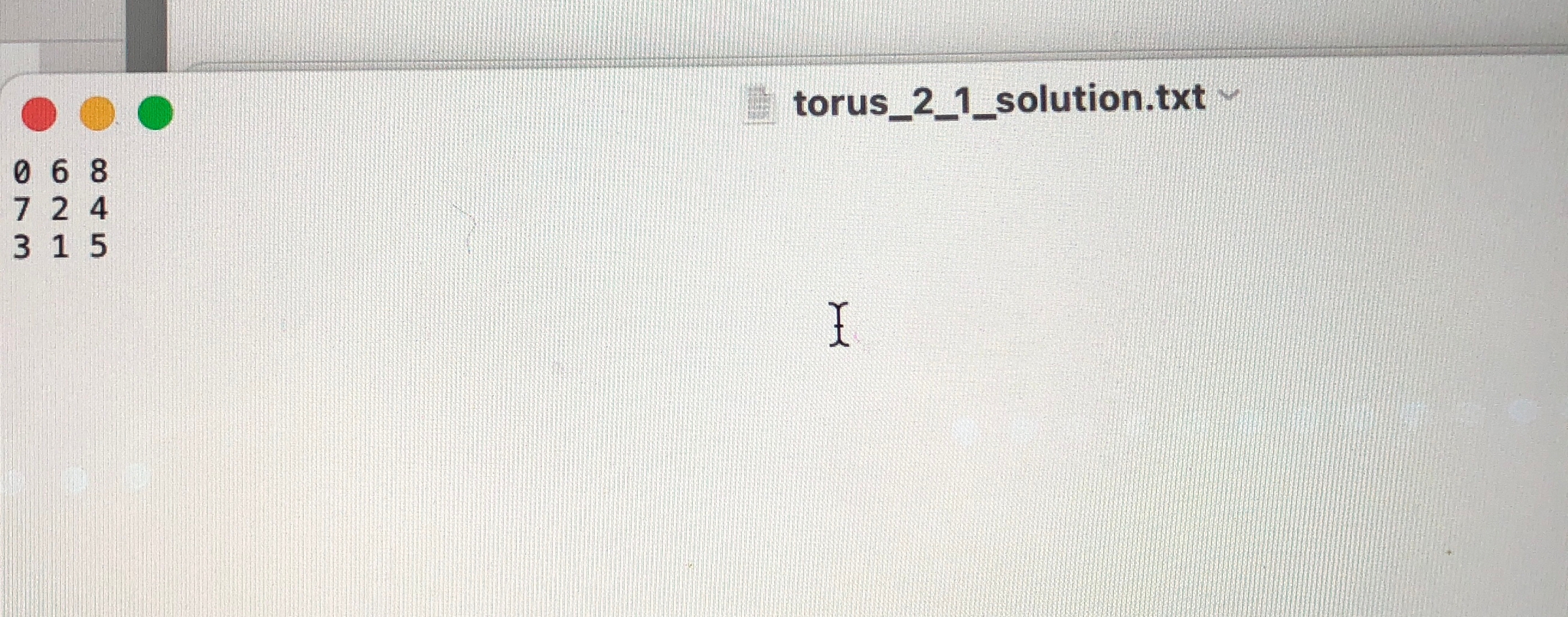
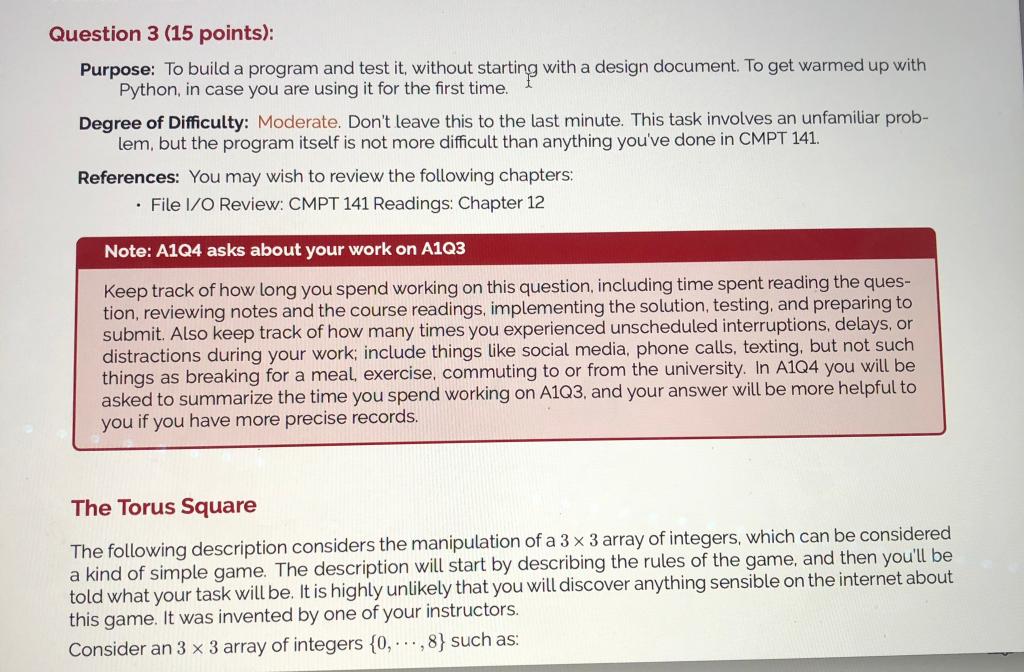
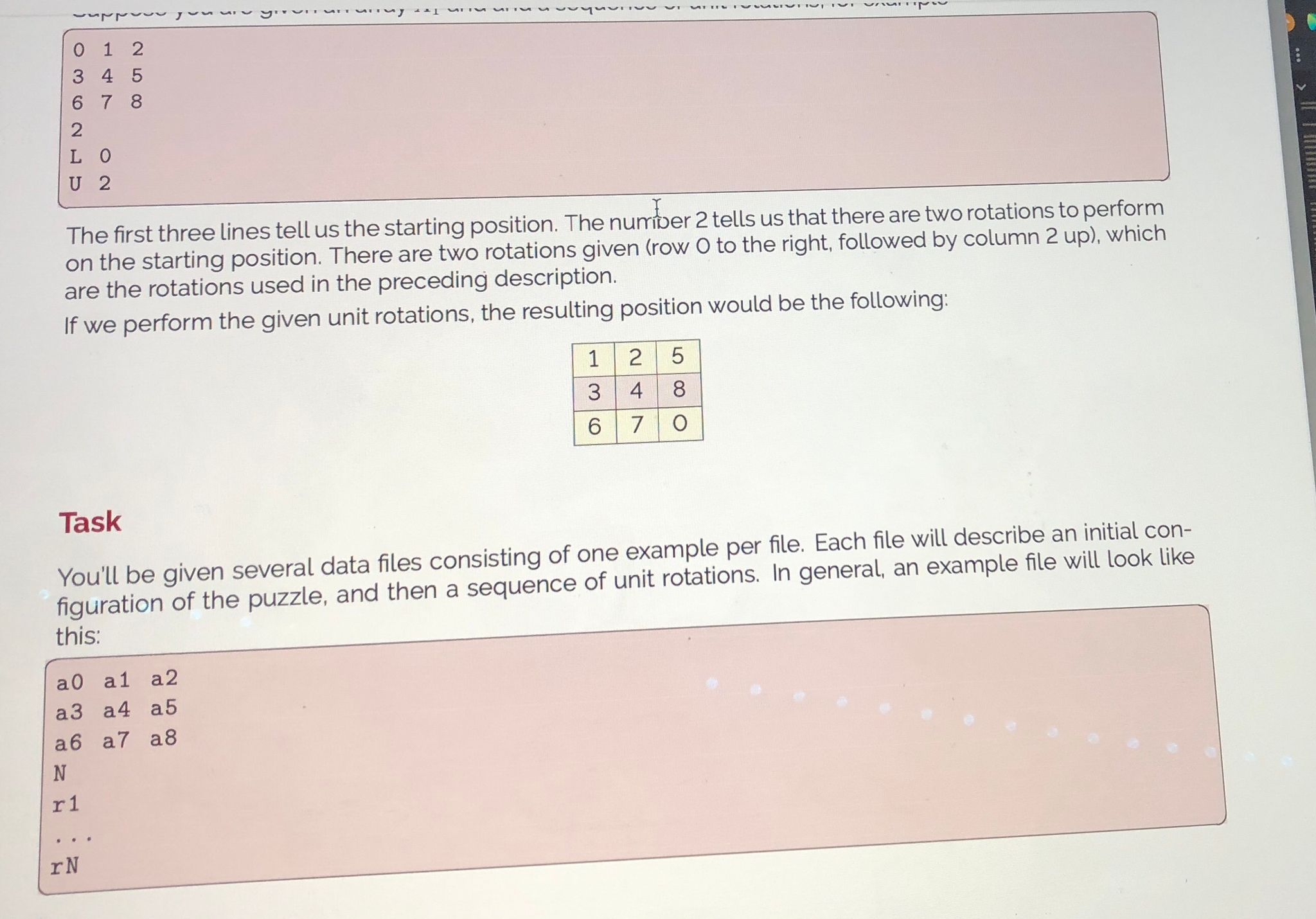
Question 3 (15 points): Purpose: To build a program and test it, without starting with a design document. To get warmed up with Python, in case you are using it for the first time. Degree of Difficulty: Moderate. Don't leave this to the last minute. This task involves an unfamiliar problem, but the program itself is not more difficult than anything you've done in CMPT 141. References: You may wish to review the following chapters: - File I/O Review: CMPT 141 Readings: Chapter 12 Note: A1Q4 asks about your work on A1Q3 Keep track of how long you spend working on this question, including time spent reading the question, reviewing notes and the course readings, implementing the solution, testing, and preparing to submit. Also keep track of how many times you experienced unscheduled interruptions, delays, or distractions during your work; include things like social media, phone calls, texting, but not such things as breaking for a meal, exercise, commuting to or from the university. In A1Q4 you will be asked to summarize the time you spend working on A1Q3, and your answer will be more helpful to you if you have more precise records. The Torus Square The following description considers the manipulation of a 33 array of integers, which can be considered a kind of simple game. The description will start by describing the rules of the game, and then you'll be told what your task will be. It is highly unlikely that you will discover anything sensible on the internet about this game. It was invented by one of your instructors. Consider an 33 array of integers {0,,8} such as: This is a kind of a puzzle, where we allow rows to be shifted left or right, and columns to be shifted up or down. We will call these actions unit rotations, for reasons that will be clarified immediately. A unit rotation is simply a shift of all the elements of a row (or column) by one position. For example, we can rotate the top row of the previous example one position to the right to get the following: Notice that the integer 2 that was on the end of the row moved to the front after the rotation to the right. Because the number 2 moved to the front of the row, we call it a rotation. Similarly, we can rotate the bottom row one position to the left to get the following: Notice that the integer 6 that was on the front of the row moved to the end after the rotation to the left. Rotations of a row can be one position right, or one position left. Rotations of a column can be one position up, or one position down. When a column is rotated up, the value on the top of the column is moved to the bottom of the column; all other elements are moved one place upwards. Because we only consider one position left, right, up, or down, we call it a unit rotation. When a row (or column) is rotated, only that row (or column) is rotated; all other rows (or columns) remain unchanged. These unit rotations can be performed in sequences, one after another, which result in the numbers moving around the puzzle array. We will represent each possible rotation with a code, which we will motivate by example, and then define carefully after the example. A unit rotation of the first row to the right will be represented by the string ' R0 '. The first letter ' R ' indicates that a row is rotated to the right. The digit ' 0 ' indicates that the first row is rotated. In general, a rotation will consist of a single letter followed by a single digit. - ' Ri ' means rotate row i to the right one position. - 'L i ' means rotate row i to the left one position. - 'U i ' means rotate column i up one position. - 'D i ' means rotate column i down one position. Here, i has to be a valid row or column index, that is: 0, 1, 2. Now that we have a code for the rotations, we can write sequences of rotations with this code. Suppose you are given an array A1 and and a sequence of unit rotations, for example 0362LU14702258 The first three lines tell us the starting position. The number 2 tells us that there are two rotations to perform on the starting position. There are two rotations given (row 0 to the right, followed by column 2 up), which 0362LU14702258 The first three lines tell us the starting position. The numiver 2 tells us that there are two rotations to perform on the starting position. There are two rotations given (row 0 to the right, followed by column 2 up), which are the rotations used in the preceding description. If we perform the given unit rotations, the resulting position would be the following: Task You'll be given several data files consisting of one example per file. Each file will describe an initial confiauration of the puzzle, and then a sequence of unit rotations. In general, an example file will look like The first three lines are the starting position of the puzzle array. Assume these will be numbers, in the range 0-8. The 4th line tells you the number of rotatichs to perform, and the remaining N lines describe each rotation (using the code above). Yourjob is to read the file, perform the rotations, and display the array showing the effect of all the rotations done in the sequence given. For example, if the input file contains the following example: 0362LU14702258 your program should read the file, perform the rotations, and finally display the result: 136247580 Data files On Canvas you will find 2 ZIP files for your use in this question: - a1q3Examples. zip Contains 15 example files, with rotation sequences of different lengths. The filenames are torus_N_i.txt, where N tells you how long the rotation sequence is, and i is an index. There are 3 examples for each N. - a1q3Solutions.zip Contains 10 files that show the solutions for most of the examples. The solution file torus_N_i_solution.txt matches the example file torus_N_i.txt. We're not giving you solution files for all the examples, so that you have to be more thoughtful about assessing your work. Data files On Canvas you will find 2 ZIP files for your use in this question: - a1q3Examples.zip Contains 15 example files, with rotation sequences of different lengths. The filenames are torus_ Ni.txt, where N tells you hoy long the rotation sequence is, and i is an index. There are 3 examples for each N. - a1q3Solutions .zip Contains 10 files that show the solutions for most of the examples. The solution file torus_N_i_solution.txt matches the example file torus_N_i.txt. We're not giving you solution files for all the examples, so that you have to be more thoughtful about assessing your work. You should be able to open ZIP files using software on any lab computer, and on your personal computer as well. If not, the ZIP format is standard, and File Compression utilities are easily downloaded from your favourite app store. What to Hand In - Your implementation of the program: a1q3.py. - If you wrote a test script, hand that in too, calling it a1q3_testing.py Be sure to include your name, NSID, student number, course number and laboratory section at the top of all documents. Evaluation - 10 marks: Your program works. - 5 marks: Your program is well-documented. \( \begin{array}{llll} & 0 & 0 \\ \text { Q } & 6 & 7 \\ 2 & 4 & 5 \\ 3 & 1 & 8 \\ 2 & & \text { torus_2 1.txt } \\ \text { D } & 2 & \\ \mathrm{R} & 1\end{array} \) torus_2_1_solution.txt