JAVA

1. Suppose you are given the following set of keys (111, 114, 118, 95, 99, 113, 128, 117, 115, 99) to insert into a hash table that holds exactly 11 values. Which index positions would those keys map to according to h = (x + i*(7 x mod 7)) mod 11?

2. Draw the minHeap that results from adding the following integers (34, 40, 58, 45 100 87 65 32 1 16 7).

3. Starting with the resulting tree from Exercise 2, draw the minHeap that results from performing a remove root operation.

4. Repeat Exercise 2 by using the same numbers to create a new maxHeap and remove the root from the maxHeap.

5. Draw the undirected graph that is represented by the following:

vertices: 1, 2, 3, 4, 5, 6, 7

edges: (1, 6), (1, 2), (2, 4), (2, 7), (3, 5), (4, 3), (4, 5), (6, 3), (5, 7), (6, 7), (3, 2)

6. Write a matrix representation of the Exercise 5 graph.

7. Is the graph from Exercise 5 connected? Is it complete?

8. List all of the cycles in the graph from Exercise 5.

9. Use the resulting graph of Exercise 5. Starting from vertex 1 and apply breadth-first search traversal by visiting the vertex according to increasing order.

10. Use the resulting graph of Exercise 5. Starting from vertex 1 and apply depth-first search traversal by visiting the vertex according to increasing order.

11. Draw a spanning tree for the graph of Exercise 5.

12. Using the same data from Exercise 5, draw the resulting directed graph.

13. Is the directed graph of Exercise 12 connected? Is it complete?

14. Apply Prim and Kruskal algorithms to the following graph and find the minimum spanning tree. Show your finding over the graph by marking the edges.

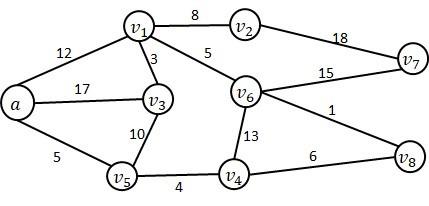
15. Starting from vertex a and apply Dijkstra's algorithm to find the shortest path from a to the other vertexes for the above graph. Show your finding over the graph by marking the edges.