JAVA CODING PLEASE HELP.
THANK YOU
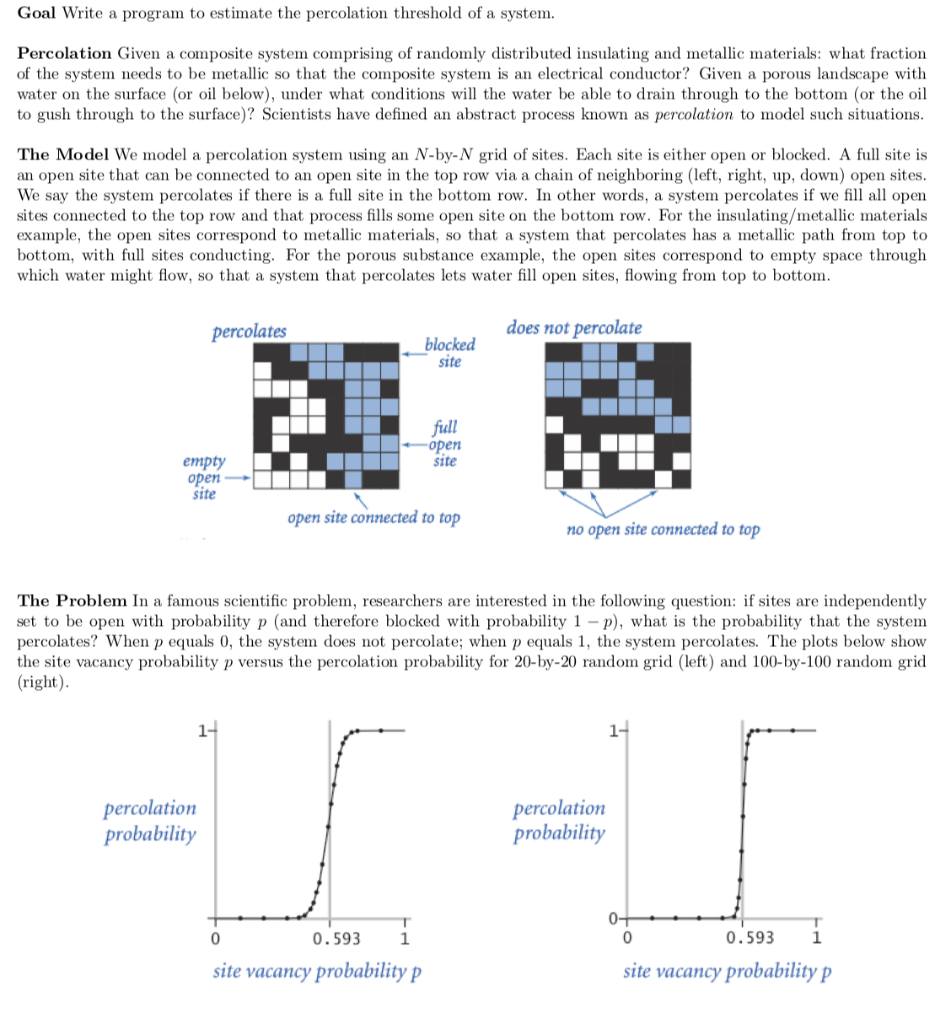
Goal Write a program to estimate the percolation threshold of a system. Percolation Given a composite system comprising of randomly distributed insulating and metallic materials: what fraction of the system needs to be metallic so that the composite system is an electrical conductor? Given a porous landscape with water on the surface (or oil below), under what conditions will the water be able to drain through to the bottom (or the oil to gush through to the surface)? Scientists have defined an abstract process known as percolation to model such situations. The Model We model a percolation system using an N-by-N grid of sites. Each site is either open or blocked. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. We say the system percolates if there is a full site in the bottom row. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row. For the insulating/metallic materials example, the open sites correspond to metallic materials, so that a system that percolates has a metallic path from top to bottom, with full sites conducting. For the porous substance example, the open sites correspond to empty space through which water might flow, so that a system that percolates lets water fill open sites, flowing from top to bottom. percolates does not percolate blocked site full open site empty open site open site connected to top no open site connected to top The Problem In a famous scientific problem, researchers are interested in the following question: if sites are independently set to be open with probability p (and therefore blocked with probability 1-p), what is the probability that the system percolates? When p equals 0, the system does not percolate; when p equals 1, the system percolates. The plots below show the site vacancy probability p versus the percolation probability for 20-by-20 random grid (left) and 100-by-100 random grid (right) percolation probability percolation probability 0 0 0.593 1 0 0.593 i site vacancy probability P site vacancy probability p When N is sufficiently large, there is a threshold value p* such that when p p*, a random N-by-N grid almost always percolates. No mathematical solution for determining the percolation threshold p* has yet been derived. Your task is to write a computer program to estimate p*. Problem 1. (Model a Percolation System) To model a percolation system, create a data type Percolation in Percolation.java with the following API: Method Description Percolation (int n) creates an N-by-N grid, with all sites blocked void open(int i, int j) opens site (ij) boolean isOpen (int i, int )) returns true if site (i, j) is open, and false otherwise boolean isFull(int i, int j) returns true if site (i, j) is full, and false otherwise int numberOfOpenSites () returns the number of open sites boolean percolates() returns true if the system percolates, and false otherwise Corner cases. By convention, the row and column indices i and j are integers between 0 and N - 1, where (0,0) is the upper-left site. Throw a java.lang.IndexOut Of BoundsException if any argument to open(), isOpen(), or isFull() is outside its prescribed range. The constructor should throw a java.lang. Illegal ArgumentException if N - */workspace/project1 $ java edu.umb. cs210.pi. Percolation data/input10.txt 56 open sites percolates $ java edu.umb. cs210.pi. Percolation data/input 10 - no.txt 55 open sites does not percolate import dsa. WeightedQuickUnionUF; import stdlib.In; import stdlib.Stdout; // Models an N-by-N percolation system. public class Percolation { // Creates an N-by-N grid, with all sites blocked. public Percolation(int N) { // Opens site (i, j) if it is not open already. public void open (int i, int j) { // Checks if site (i, j) is open. public boolean isOpen(int i, int i) { // Checks if site (i, j) is full. public boolean isFull(int i, int j) { // Returns the number of open sites. public int numberOfOpenSites() { // Checks if the system percolates. public boolean percolates() { // Returns an integer ID (1...N) for site (i, j). protected int encode(int i, int j) { // Test client. [DO NOT EDIT] public static void main(String[] args) { String filename = args[0]; In in = new In(filename); int N = in.readInt(); olation perc = new Percolation (N); while (!in.isEmpty()) { int i = in.readInt(); int j = in.readInt(); perc.open(i, j); Stdout.println(perc. numberOfOpenSites() + " open sites"); if (perc.percolates() { Stdout.println("percolates"); else { Stdout.println("does not percolate"); // Check if site (i, j) optionally specified on the command line // is full. if (args.length == 3) { int i = Integer.parseInt(args [1]); int j = Integer.parseInt(args[2]); Stdout.println(perc.isFull(i, j)); Goal Write a program to estimate the percolation threshold of a system. Percolation Given a composite system comprising of randomly distributed insulating and metallic materials: what fraction of the system needs to be metallic so that the composite system is an electrical conductor? Given a porous landscape with water on the surface (or oil below), under what conditions will the water be able to drain through to the bottom (or the oil to gush through to the surface)? Scientists have defined an abstract process known as percolation to model such situations. The Model We model a percolation system using an N-by-N grid of sites. Each site is either open or blocked. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. We say the system percolates if there is a full site in the bottom row. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row. For the insulating/metallic materials example, the open sites correspond to metallic materials, so that a system that percolates has a metallic path from top to bottom, with full sites conducting. For the porous substance example, the open sites correspond to empty space through which water might flow, so that a system that percolates lets water fill open sites, flowing from top to bottom. percolates does not percolate blocked site full open site empty open site open site connected to top no open site connected to top The Problem In a famous scientific problem, researchers are interested in the following question: if sites are independently set to be open with probability p (and therefore blocked with probability 1-p), what is the probability that the system percolates? When p equals 0, the system does not percolate; when p equals 1, the system percolates. The plots below show the site vacancy probability p versus the percolation probability for 20-by-20 random grid (left) and 100-by-100 random grid (right) percolation probability percolation probability 0 0 0.593 1 0 0.593 i site vacancy probability P site vacancy probability p When N is sufficiently large, there is a threshold value p* such that when p p*, a random N-by-N grid almost always percolates. No mathematical solution for determining the percolation threshold p* has yet been derived. Your task is to write a computer program to estimate p*. Problem 1. (Model a Percolation System) To model a percolation system, create a data type Percolation in Percolation.java with the following API: Method Description Percolation (int n) creates an N-by-N grid, with all sites blocked void open(int i, int j) opens site (ij) boolean isOpen (int i, int )) returns true if site (i, j) is open, and false otherwise boolean isFull(int i, int j) returns true if site (i, j) is full, and false otherwise int numberOfOpenSites () returns the number of open sites boolean percolates() returns true if the system percolates, and false otherwise Corner cases. By convention, the row and column indices i and j are integers between 0 and N - 1, where (0,0) is the upper-left site. Throw a java.lang.IndexOut Of BoundsException if any argument to open(), isOpen(), or isFull() is outside its prescribed range. The constructor should throw a java.lang. Illegal ArgumentException if N - */workspace/project1 $ java edu.umb. cs210.pi. Percolation data/input10.txt 56 open sites percolates $ java edu.umb. cs210.pi. Percolation data/input 10 - no.txt 55 open sites does not percolate import dsa. WeightedQuickUnionUF; import stdlib.In; import stdlib.Stdout; // Models an N-by-N percolation system. public class Percolation { // Creates an N-by-N grid, with all sites blocked. public Percolation(int N) { // Opens site (i, j) if it is not open already. public void open (int i, int j) { // Checks if site (i, j) is open. public boolean isOpen(int i, int i) { // Checks if site (i, j) is full. public boolean isFull(int i, int j) { // Returns the number of open sites. public int numberOfOpenSites() { // Checks if the system percolates. public boolean percolates() { // Returns an integer ID (1...N) for site (i, j). protected int encode(int i, int j) { // Test client. [DO NOT EDIT] public static void main(String[] args) { String filename = args[0]; In in = new In(filename); int N = in.readInt(); olation perc = new Percolation (N); while (!in.isEmpty()) { int i = in.readInt(); int j = in.readInt(); perc.open(i, j); Stdout.println(perc. numberOfOpenSites() + " open sites"); if (perc.percolates() { Stdout.println("percolates"); else { Stdout.println("does not percolate"); // Check if site (i, j) optionally specified on the command line // is full. if (args.length == 3) { int i = Integer.parseInt(args [1]); int j = Integer.parseInt(args[2]); Stdout.println(perc.isFull(i, j))
