*JAVA*

Consider the Fibonacci numbers: F(n) = F(n 1) + F(n 2), n > 1; F(1) = 1; F(0) = 0.

b). Write a recursive function/procedure to compute F(n) with time complexity O(n) (more precisely, the time complexity should be O(nA(n)) when n is large, where A(n) is the complexity of adding F(n1) and F(n2)). Implement your solution and print F(i20), where 0 i 25, as output. This program must be able to compute F(n) precisely for n 500.

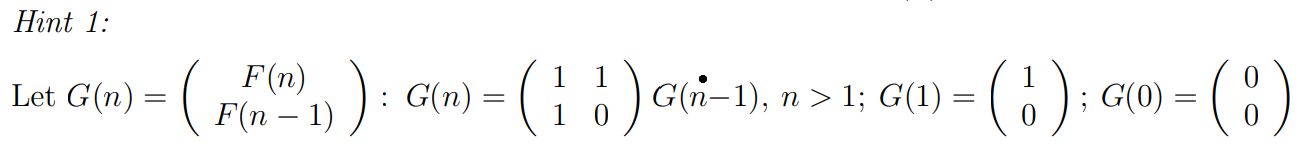
Hint 2: Can you use a primitive type to store F(500)?

Hint 1: Let G(n) = ( Fin-1 ) (ren), ) : g(n) = (1 o) - G(n) = ( 1 ) C(n=1), n > 1; G(1) = ( 6 ); (0) = ( 7 ) Hint 1: Let G(n) = ( Fin-1 ) (ren), ) : g(n) = (1 o) - G(n) = ( 1 ) C(n=1), n > 1; G(1) = ( 6 ); (0) = ( 7 )