Java Recurrence Assignment Help!!


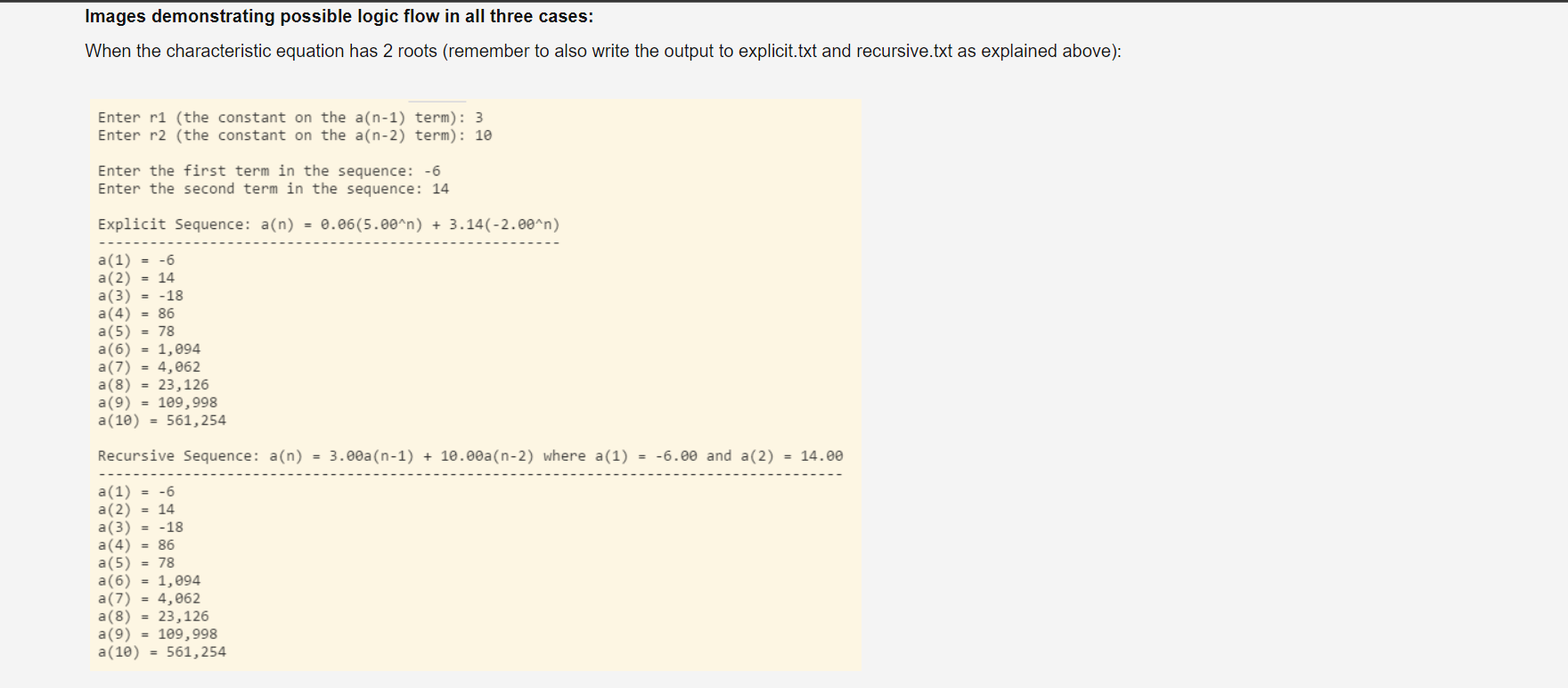
- LHD2Recurrence (i.e. linearly homogenous degree-2 recurrence relation) - Attributes - data to store all of the characteristics of the recursive sequence and the linear sequence (i.e. r1, r2, a1, a2, u, v, s1, s2) - DecimalFormat objects to format the output (sequence definitions should displayed with 2 decimal places in all cases and sequence elements should be displayed with no decimal places) - any other pertinent data - Behaviors - appropriate constructor - a method that determines the characteristics of the explicit equation (this will utilize the SystemOfTwo and QuadraticEquation classes defined below) - methods that return a String representation of the sequence definitions - methods that return the actual sequence elements - any other necessary supporting methods - MyClass - driver that drives the flow of the logic as in the images below as follows: - prompts the user for the information associated with a second-degree linearly homogenous recurrence relation - uses the classes above to determine the corresponding equivalent explicit sequence - neatly displays each sequence and the first 10 elements generated from each sequence - writes the output to output files as follows: - the explicit sequence and elements are written to a file called explicit.txt - the recursive sequence and elements are written to a file called recursive.txt - if the roots of the quadratic equation are complex, no output files should be generated - Class Name: QuadraticEquation (this class was written in component 1) - Attributes - three private variables to store the: - quadratic coefficient (i.e. the coefficient on the x2 term) - linear coefficient (i.e. the coefficient on the x term) - the constant of a quadratic equation - Behaviors - three methods as follows: - default constructor that assigns the value 1 to each of the three attributes - appropriate alternate constructor - a method that calculates the roots of the quadratic equation and returns them in an ArrayList (this will ultimately have 0, 1, or 2 elements depending on the number of solutions) - Class Name: SystemOfTwo (this class was written in component 2) - Attributes - data to store all 6 coefficients and constants associated with a system of linear equations with two unknowns - Behaviors - appropriate constructor - method that determines the solution to the system of equations and returns the information as an instance of the Point class (defined below) - Note - you do not need to check for systems of parallel lines, or systems of two occurrences of the same line - Class Name: Point (this class was written in component 2) - Attributes - data to store the x and y coordinates of the Point - Behaviors - appropriate constructor - getters and setters for each coordinate Images demonstrating possible logic flow in all three cases: When the characteristic equation has 2 roots (remember to also write the output to explicit.txt and recursive.txt as explained above): Enter r1 (the constant on the a(n1) term): 3 Enter r2 (the constant on the a(n2) term): 10 Enter the first term in the sequence: 6 Enter the second term in the sequence: 14 Explicit Sequence: a(n)=0.06(5.00n)+3.14(2.00n) a(1)=6 a(2)=14 a(3)=18 a(4)=86 a(5)=78 a(6)=1,094 a(7)=4,062 a(8)=23,126 a(9)=109,998 a(10)=561,254 Recursive Sequence: a(n)=3.00a(n1)+10.00a(n2) where a(1)=6.00 and a(2)=14.00 a(1)=6 a(2)=14 a(3)=18 a(4)=86 a(5)=78 a(6)=1,094 a(7)=4,062 a(8)=23,126 a(9)=109,998 a(10)=561,254









