just need help with #7
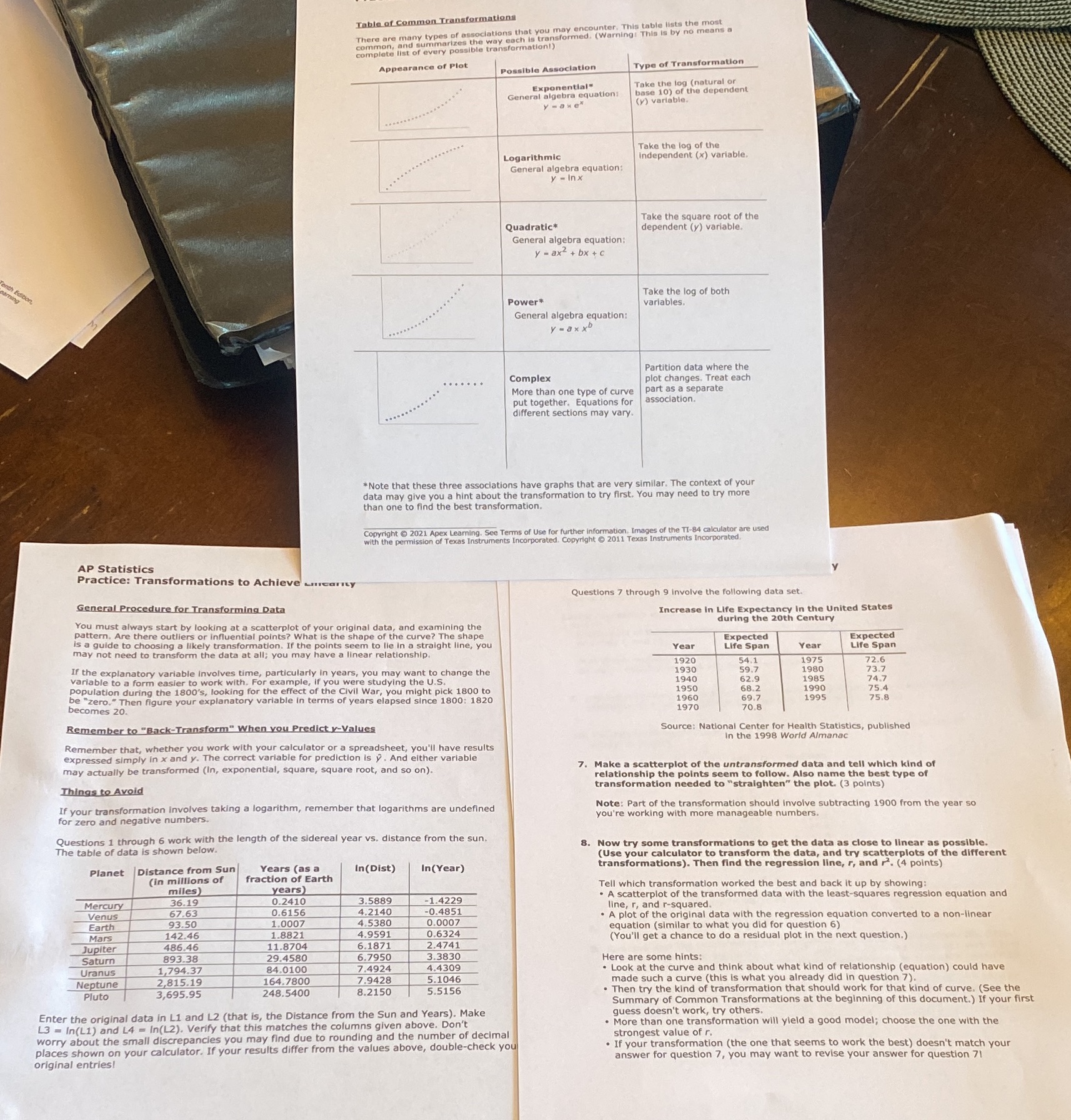
Table of Common Transformations There are many types of associations that you may encounter. This table lists the most rmed. (Warning: This is by no means a complete list of ever Appearance of Plot Possible Association Type of Transformation Exponential" Take the log (natural or General algebra equation: se 10) of the dependent y - ax ex () variable, Take the log of the Logarithmic ndependent (x) variable. General al y - Inx Take the square root of the Quadratic* dependent (y) variable. General algebra equation: y - ax2+ bx + c Take the log of both Power* variables . ................".". General algebra equation: y - ax xb Partition data where the Complex plot changes. Treat each ............ .... More than one type of curve part as a separate put together. Equations for association. different sections may vary. *Note that these three associations have graphs that are very sim are very similar. The context of your data may give you a hint a it the transformation to try first. You may need to try more than one to find the best transformation. ages of the TI-84 calculator are used Copyright @ 2021 Apex Learning. See Terms of Use for further information This Instruments Incorporated. with the permission of Texas Instruments Incorporated. Copyright @ 2011 Texas Instrument AP Statistics Practice: Transformations to Achieve LinearIty Questions 7 through 9 Involve the following data set. General Procedure for Transforming Data Increase In Life Expectancy In the United States You must always start by looking at a scatterplot of your original data, and examining the during the 20th Century are there outliers or influential points? what is the shape of the curve? The shape Expected ed to transform the data at all; you may ar relationship. Year Life Span Year Life Span 1920 54.1 If the explanatory variable involves time, particularly in years, you may want to change the 1975 59.7 72.6 variable to a form easier to work with. For example, If you were studying the U.S. 62.9 74.7 population during the 1800's, looking for the effect of the Civil War, you might pick 1 1990 75.4 be "zero." Then figure your explanatory variable in terms of years .you 68.2 75.8 becomes 20. of years elapsed since 1800: 1820 69.7 1970 70.8 1995 Remember to "Back-Transform" When you Predict y-Values Source: National Center for Health Statistics, published In the 1998 World Almanac er you work with your calculator or a spreadsheet, you'll have results expressed simply in x and y. The correct variable for prediction is y . And either variable may actually be transformed (In, exponential, square, square root, and so on). 7. Make a scatterplot of the untransformed data and tell which kind of relationship the points seem to follow. Also name the best type of Things to Avoid transformation needed to "straighten" the plot. (3 points) If your transformation involves taking a logarithm, remember that logarithms are undefined : Part of the transformation should involve subtracting 1900 from the year so for zero and negative numbers. you're working with more manageable numbers. Questions 1 through 6 work with the length of the sidereal year vs. distance from the sun. The table of data is shown below. B. Now try some transformations to get the data as close to linear as possible. (Use your calculator to transform the data, and try scatterplots of the different Planet Distance from Sun Years (as a In (Dist) In (Year) transformations). Then find the regression line, r, and r. (4 points) (in millions of fraction of Earth miles years Tell which transformation worked the best and back it up by showing: Mercury 21.63 0.2410 3.5889 1.4229 A scatterplot of the transformed data with the least-squares regression equation and Venus 0.6156 4.2140 -0.4851 93.50 1.0007 4.5380 0.0007 A plot of the original data with the regression equation converted to a non-linear Mars 142.46 1.8821 4.9591 0.6324 uation (similar to what you did for question 6) Jupiter 486.46 11.8704 6.1871 2.4741 (You'll get a chance to do a residual plot in the next question.) Saturn 893.38 29.4580 6.7950 3.3830 Here are some hints: Uranus 1,794.37 84.0100 7.4924 4.4309 Neptune 2,815.19 7.9428 Look at the curve and think about what kind of relationship ( 164.7800 5.1046 248.5400 8.2150 5.5156 made such a curve (this is what y s is what you already did in question 7). pluto 3,695.95 Then try the kind of transformation that should work for that kind of curve. (See the Summary of Common Transformations at the beginning of this document.) If your first Enter the original data in L1 and L2 (that is, the Distance from the Sun and Years). Make guess doesn't work, try others. 13 - In(L1) and L4 = In(L2). Verify that this matches the columns given above. Don't More than one transformation will yield a good model; choose the one with the worry about the small discrepancies you may find due to rounding and the number of decimal strongest places shown on your calculator. If your results differ from the values above, double-check you If your transformation (the one that seems to work the best) doesn't match your original entries! answer for question 7, you may want to revise your answer for question 71