KINDLY PLEASE DIGITALIZED IT

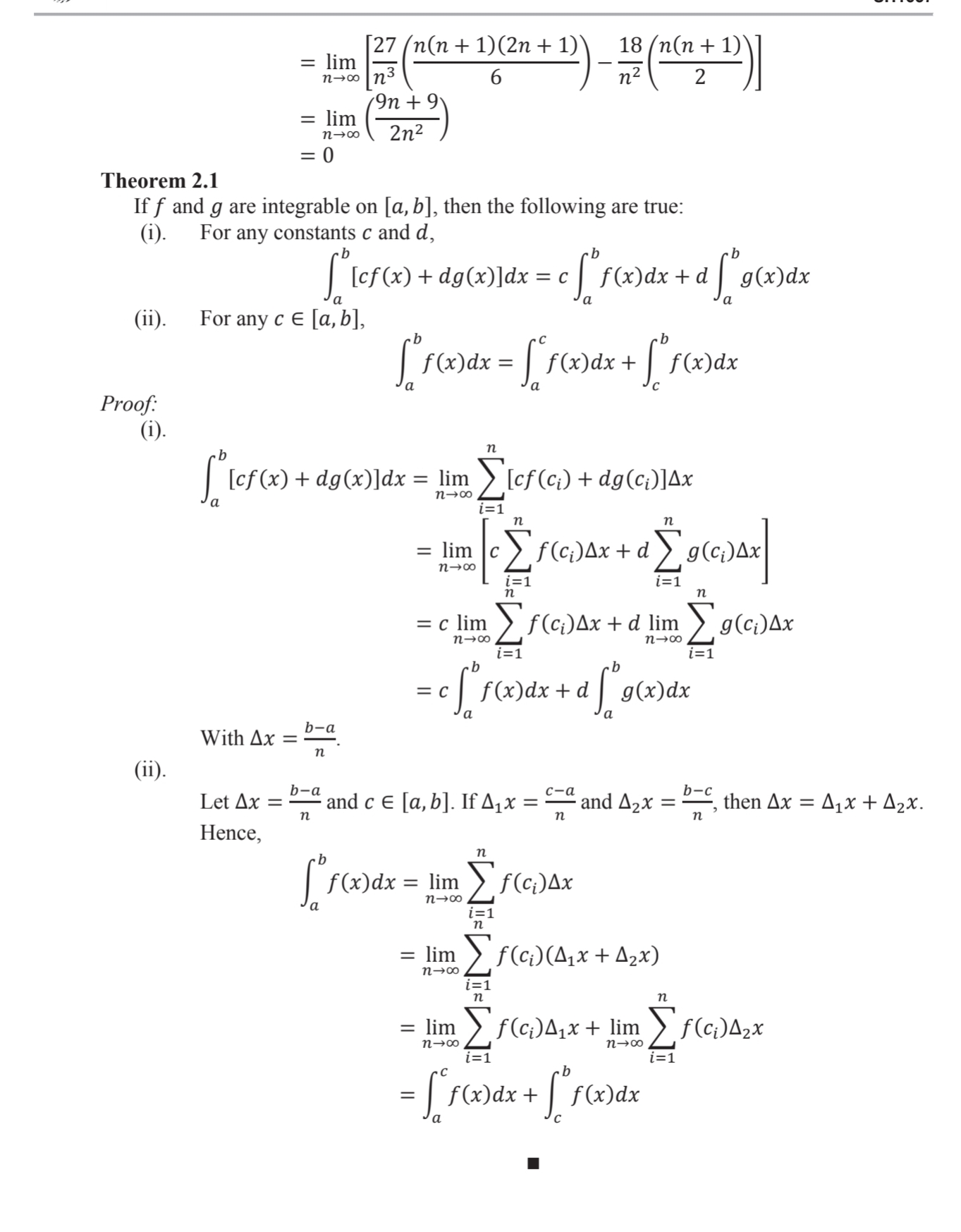
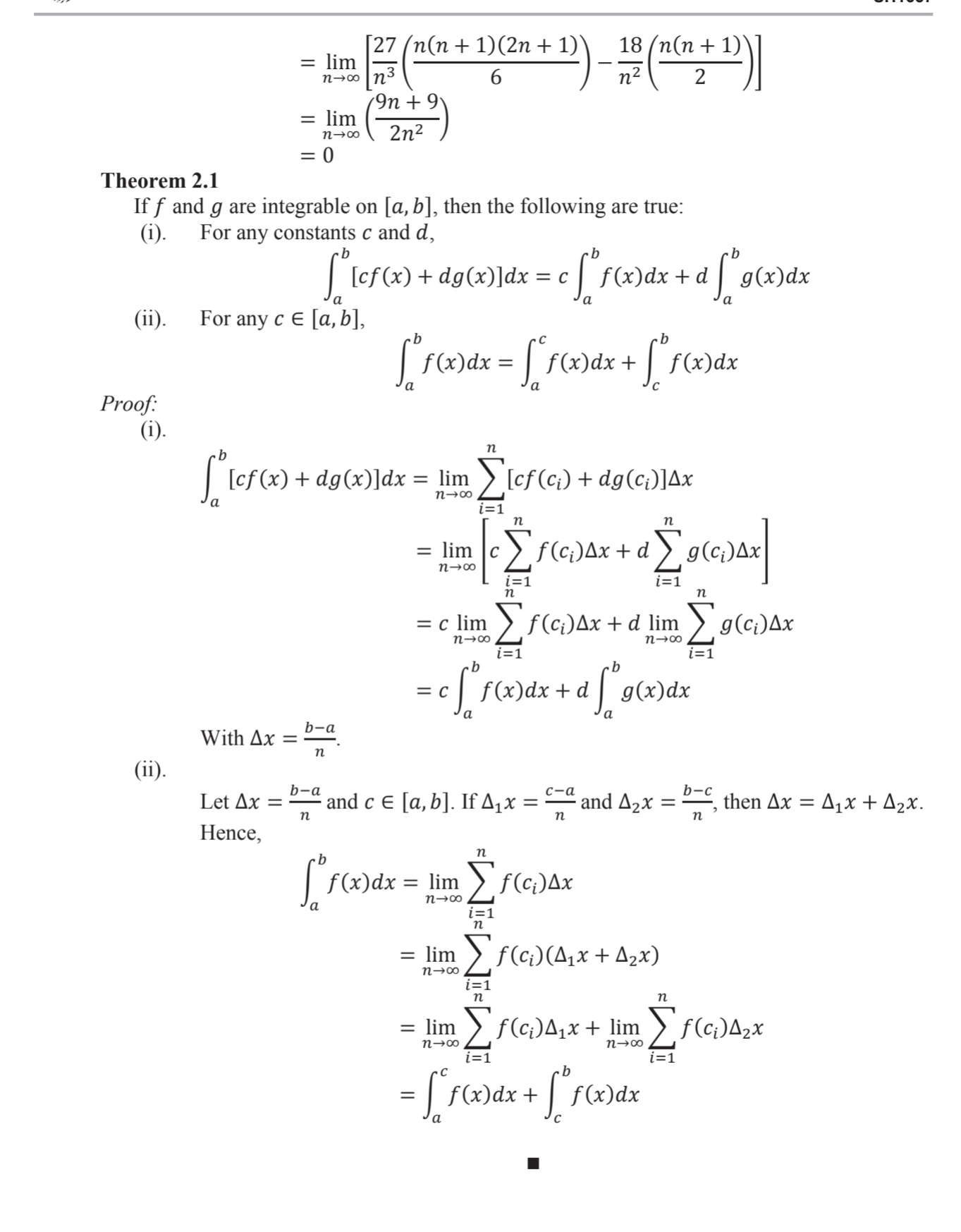
11- Find the Area between the curve y=x(x-3) and the ordinates x=0 and x=5. Note: (hint) The Graph shows 2 regions. Get first the area of each region before adding it together.The Denite Integral Riemann Sum We introduce a method of appr0ximating the area beneath the graph of y = f (x) and above the x-axis on an interval [a, b]. Assume f (x) 2 0 and f is continuous on the interval [a, b]. This method revolves around what is known as Riemann sum. Computing the Riemann Sum I We start by dividing the interval into 11 equal pieces, which we will call regular partition of [a, b]. The width of each partition in the interval is E = Ax. The points it in the partition will be denoted as xi = x0 + iAx,fori = 1,2, ...,n where x0 = a and xn = b. 0 We choose evaluation points c1,c2, ...,cn where Ci is any point in the subinterval [xi_1,xi], for i = 1,2, ...,n, and we compute for corresponding images f(C1),f(C2), "Hf-(cu)- . We compute for the Riemann sum given by the formula 11 21mm (1.1) i=1 Example 1 Approximate the area under f (x) = 2x 21:2 on the interval [0.1] using 10 rectangles. Use midpoints of each interval as evaluation points. Solution: 10 The partition divides [0,1] into 10 intervals, each of width Ax = T = 0.1. The points in the partition are 0, 0.1, 0.2, ...,0.9,1. The evaluation points Ci are 005,015,025,...,0.85,0.95, with corresponding pre-images f(0.05)=0.095, f(0.15) = 0.255, f(0.25) = 0.375), f(0.85) = 0.255, f(0.95) = 0.095. Hence, if A = area of rectangle, then A z if(ci)x ' 1 =l[=f(0.05) + f(0.15) + f(0.25) + + f(0.85) + f(0.95)](0.1) = (0.095 + 0.255 + 0.375 + + 0.255 + 0.095)(0.1) = 0.335 For functions with negative values, f (Ci) 5 0- Hence, Area of it" rectangle = |f(c;-)|Ax = f (cam: In general, A z ZIcle (1.2) i=1 II. The Definite Integral For any value of t where f (t) 2 0, the exact area between the curve and the x-axis is given by the limit as n - co of equation (1.1). Definition 2.1 For any function f defined on [a, b], the definite integral of f from a to b is [ foodx = lim [f(G)Ax (2.1) i=1 whenever the limit exists and is the same for every choice of evaluation points, C1, C2, ..., Cn. When the limit exists, we say that f is integrable on [a, b]. f(x) in (2.1) is called the integrand. Note that a function continuous on [a, b] is integrable on [a, b]. Example 2.1 Determine the definite integral of f (x) = x2 - 2x from 0 to 3. Solution: 3 -0 Ax = 3 n n We then have XO = 0 w C1 = X1 = 0+ Ax =. n 3i Ci = Xi = 0 + iAx = - Cn = Xn = 3 Hence, [ fox)ax = lim 146 _ F ( c : )AX = lim 912 = I n-0o 1 2 n n n 2712 18i = lim n-+0o n3 n2 18 = lim n 227 n(n + 1)(2n + 1) 18 (n + 1) = lim n3 6 n 2 2 9n + 9 = lim n-0o 2n2 = 0 Theorem 2.1 If f and g are integrable on [a, b], then the following are true: (i). For any constants c and d, (ii). For any c E [a, b], Proof: (i). [[of (x) + dg (x)]dx = lim > [of (c;) + dg(c;)]Ax n-co = lim 00 - U i=1 1=1 = c lim n-+0o f ( c)Ax + d lim h-d > 9 (CD)AX i=1 1= 1 = cf f(x)ax + d g(x)dx With Ax = - (ii). Let Ax = -" and c E [a, b]. If Aix = and Azx = -, then Ax = Aix + 2x. Hence, ['f()ax = lim EF()Ax = lim n->co f ( ci ) ( 4 , x + 42x ) = lim f( c)Ax+ lim n -+co n-0o = [ f()dx + f(x)dxSH1657 The solution to the definite integral gives you the signed area of a region, that is, if f (x) 2 0, then the definite integral is positive, otherwise, it is negative. In contrast, the unsigned area is always positive, that is, if A is the unsigned area between the curve f (x) and the x- axis, then A = [ if( * ) Idx (2.2) If f (x) 2 0 on [a, b], then A = Sa f(x)dx. Otherwise, A = - Sof(x)dx. Example 2.2 Let f (x) = x2 - 2x. Determine the unsigned area for 0 0. Hence, f (x) > 0 for all x E (2, 3). Therefore, if A is the unsigned area between f (x) and the x-axis for 0 f(c;)Ax Taking the limit of both sides as n - co, F(b) - F(a) will be denoted as F(x) lb. Example 3.1 e 3x Compute So (tex)z dx. Solution: Let F(x) be the antiderivative of (1tex)z. Note that the table of integrals (10 Handout 2) gives formula for integrals of forms involving a + bu. We can let a = b = 1, u = ex du = edx and use the formula. Hence, e 3x F(x )+c = (1 + ex) 2 ax (ex)2 (1 + ex)ze*dx u2 (1 + u)2 du 1 =1tu -- 1 + u 2 In|1 + ul + c 1 = ex - 1+ex - 2In|1 + ex| + C Therefore, F(x) = ex - e 3x 1tex - 2 In|1 + ex|. Since (1tex)z is continuous on [0,1], by Theorem 3.1, e 3x (1tex)z dx = 1 It ex 1 = (e 1 te - 2 In| 1 + el) - (1 - 2 -2In121) ~ 0.7091 Example 3.2 Determine the area under the curve f (x) = 2 cos 2x on the interval |- ", ]. Solution: Let F(x) be the antiderivative of 2 cos 2x. Let u = 2x, then du = 2dx. Therefore, F(x) +c =|2 cos 2xdx= cos u du = sinu + c = sin 2x + c Therefore, F(x) = sin 2x. Since 2 cos 2x is continuous on - , ", It / 4 2 cos 2x dx = sin 2x|-7/4 It / 4 = sin 2 - - sin 2 (-~) =1 - (-1) =2 Example 3.3 Determine the signed and unsigned areas between the curve f(x) = xv2 - x and the x- axis on the interval [-1,1 ]. Solution: Let F(x) be the antiderivative of f (x) and let u = 2 - x, du = -dx F (x) +c = |xv2 -xdx = - (2 -u) Vudu = - (24312 - 23/2) du = -4312 - 2u -= 1512 ) + c 4 = 3 (2 - x) 3/2 + = ( + 5 ( 2 - x ) 5/ 2 + C This implies that F(x) = -= (2 - x)3/2 + 2(2 - x)5/2. Since xV2 - x is continuous on [-1,1 ], the signed area between f (x) and the x-axis on [-1,1 ] is xV2 - xdx = F(x)121 [-$(2-1)3/2 + 3 (2- 1)5/2] - [-$(2+1)312 +3 (2+1)5/2] ~ -0.2405 To compute for the unsigned area, we first determine what region/s in [-1, 1] is f(x) 0. Thus, the unsigned area between f (x) and the x-axis on [-1,1 ] is [(xvz - xax + [ lxvz - x/dx = - [ xV2 - xdx+ xv2- xdx = -F(x)|21 + F(x)18 = F(1) -2F(0) + F(-1) [-3+31-2[-3 (2)2 + 3 (2)2] + [-3(3)312 + 3 (3)5/2] ~ 1.3908SH1657 Theorem 3.2 Let f (x) be continuous on [a, b], then [' fondx = - [ f( )dx Proof: [ f( )dx = F(b) - F(a) = -[F(a) - F(b)] = - ( f( x)dx Definition 3.1 Let f(x) be continuous on [a, b]. The average value of f on [a, b] is given by fab = D- al "f ( dx Theorem 3.3 (Integral Mean Value Theorem) If f is continuous on [a, b], then 3 c E [a, b] for which f (c) = fab Proof: Since f is continuous on [a, b], by the Extreme Value Theorem, it achieves a minimum value m, and a maximum value M on [a, b] so that m s f(x) f(x). Example 4.1 Determine the area between the curves f(x) = -x2 + 3x and g(x) = 2x3 - x2 - 5x for x E [-2,2]. Solution: f(x) - g(x) =-2x3 + 8x = x(-2x2 + 8) =0 ifx = -2 orx = 0 or x = 2. At -1 E (-2, 0), f(x) - g(x) = -60 Hence, the area between f (x) and g(x) for x E [-2,2] is [If ( x) - 9(x)|dx = [g(x) - f(x)]dx + [f (x) - g(x)lax -2 = [2x3 - 8x]dx + [-2x3 + 8x]dx -2 = ( x4 - 4x2 ) 1 92 + ( - 7* # + 4x 2 ) 12 = -(2(-2)4 -4(-2)2) + 1-7(2)4+4(2)2) = 16 References: Minton, R. & Smith, R. (2016). Basic Calculus. McGraw Hill Education. Coburn, J. (2016). Pre-Calculus. McGraw Hill Education.Preliminary Notes Theorem 1.1 (Mean Value Theorem) Suppose f is continuous on the interval [a, b] and differentiable on the interval (a, b). Then there exists a number c E (a, b) such that f'(c) = 1( b) - f(a) b - a The Sigma Notation Let a1, d2, ..., an-1, an be a sequence of terms. We denote the sum of the terms in the sequence as [a = a, taz + . + an- 1 + an 1=1 The variable i is the index of summation. If we wish to compute the sum of the jith term up to the kth term, 1 0), or less than zero ( 0 or 0 on the interval (-co, -2) and (3, +co). References: Minton, R. & Smith, R. (2016). Basic Calculus. McGraw Hill Education. Mean Value Theorem for Integrals. ( n.d.). Retrieved from http://www.mathwords.com/m/mean_value_theorem_integrals.htm on September 19, 2016 Solving Inequalities. (n.d.). Retrieved from https://www.mathsisfun.com/algebra/inequality- solving.html on September 21, 2016. Solving Quadratic Inequalities. (n.d.). Retrieved from https://www.mathsisfun.com/algebra/inequality-quadratic-solving.html on September 21, 2016