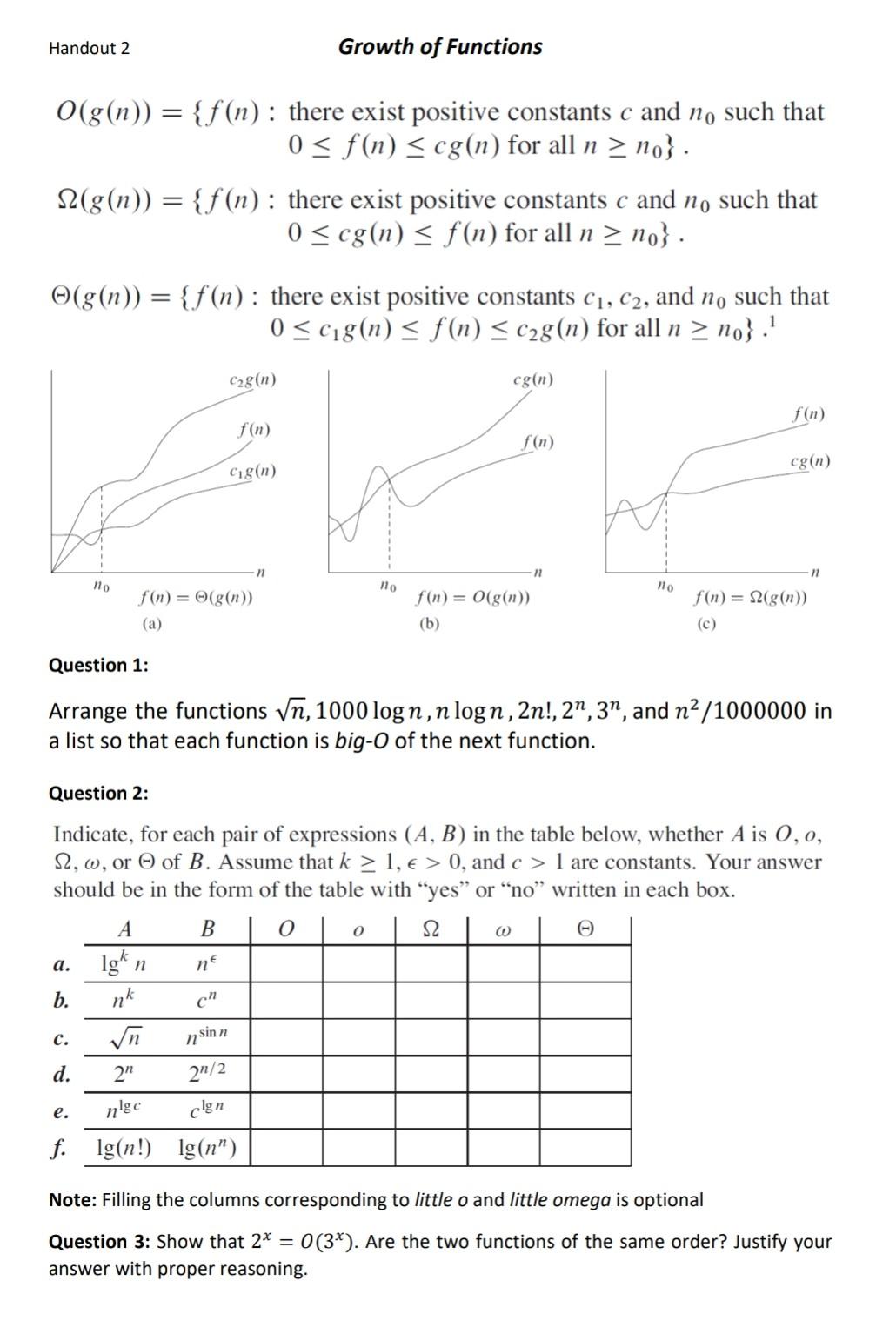
kindly solve all questions

O(g(n))={f(n) : there exist positive constants c and n0 such that 0f(n)cg(n) for all nn0}. (g(n))={f(n) : there exist positive constants c and n0 such that 0cg(n)f(n) for all nn0}. (g(n))={f(n) : there exist positive constants c1,c2, and n0 such that 0c1g(n)f(n)c2g(n) for all nn0}1 Question 1: Arrange the functions n,1000logn,nlogn,2n!,2n,3n, and n2/1000000 in a list so that each function is big- O of the next function. Question 2: Indicate, for each pair of expressions (A,B) in the table below, whether A is O,o, , , or of B. Assume that k1,>0, and c>1 are constants. Your answer should be in the form of the table with "yes" or "no" written in each box. Note: Filling the columns corresponding to little o and little omega is optional Question 3: Show that 2x=O(3x). Are the two functions of the same order? Justify your answer with proper reasoning