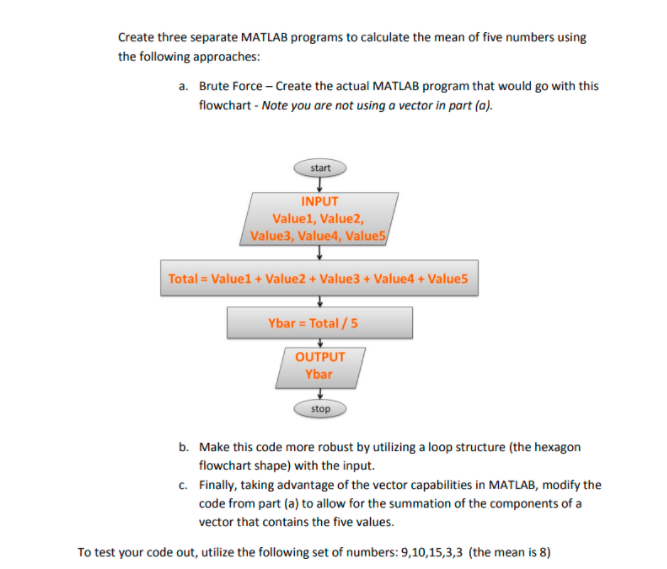
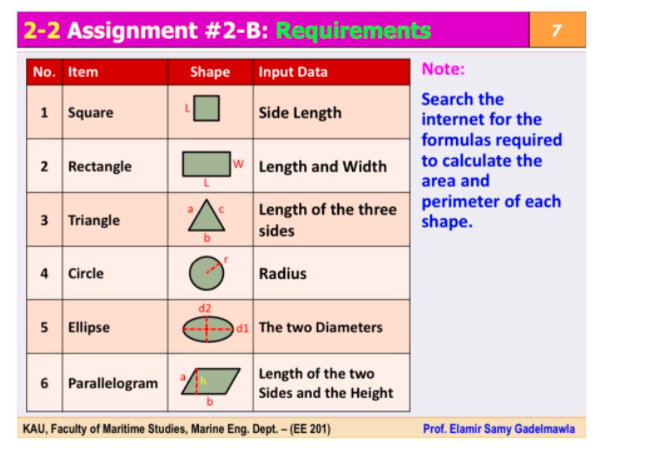
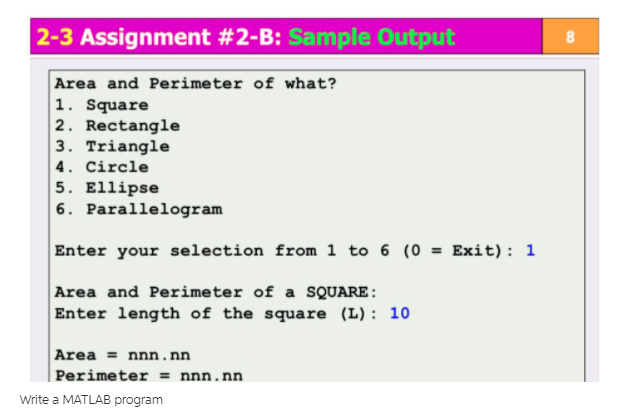
! Kindly solve the following

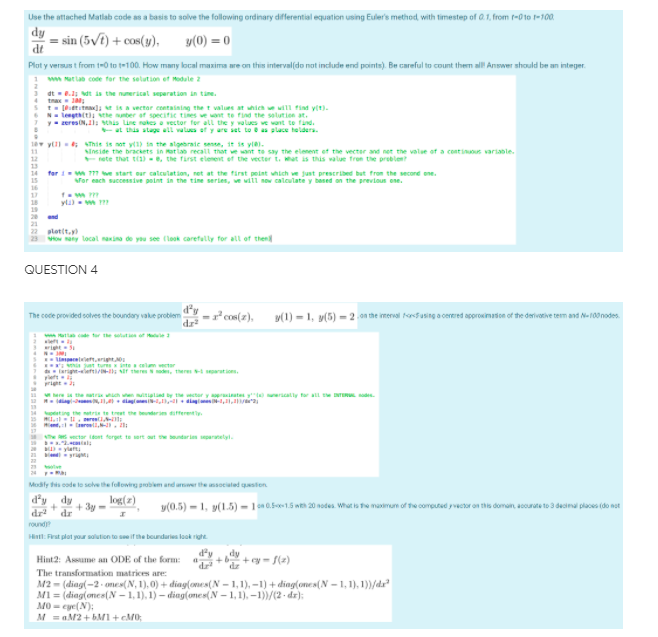
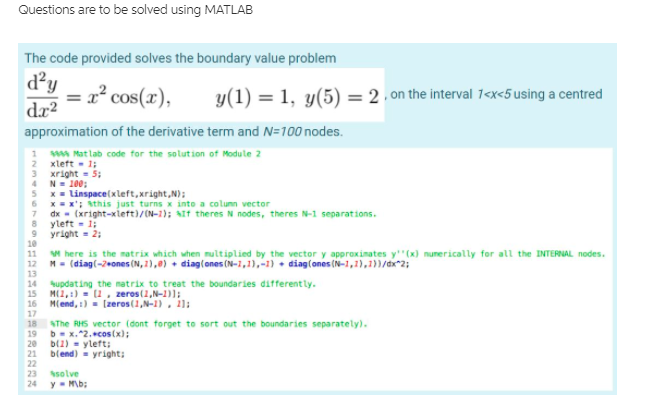
Use the aflached Matlab code as a basis to solve the following ordinary differential equation using Euler's method, with timestep of Q 1, from r-0 10 1-100 dy de = sin (5v/t) + cos(y). y(0) = 0 Plot y versus t from 1=0 to 1=100. How many local maxima are on this interval (do not include end points). Be careful to count them all Answer should be an integer. ww Matlab code for The solution of Module 2 dt = 0.Jj it is the moorical separation in time. I . iftrivial; he is a vector containing the f wilues at which we will Find vit). No keagtiltli Wthe meter of specific times we want to find the solution it. : wchis Line mobes a vector for all the y wolves we want to find. "- at this slaps all values of y are set to @ as place holder. lly pill = d; "this is not will in the algebraic sense, it is rial. Sinside the brackets in Matlab recall that we want to say the element of the vector and not the value of a continu variable. 12 "note that Will = 0, the first clement of the vector . what is this value from the problemt 14 for i w M 17 be start our calculation, not at the first point which we just prescribed but from the second one. Sfor each successive paint in the time series, we will sow calculate y based on the previous one. ITE platit,ph Whoy Silly local maxiss do you see Cloak carefully for all of them QUESTION 4 The code provided solves the boundary value problem "ros(z), (1) = 1, y(5) - 2.on the ingerwal facesfusing a centred approximation of the derivative term and ti- 107 nodes. Soph Matlab cade for the what is of Audible pright . 5; boasting tay metris to boost the bowbrin differetip via hui victor ifout forget to mart art the boundaries inparisstyle Modily ids code is solve the following problem and arrower the associated question. d'y dy + 3y - log(z) 1(0.5) = 1, p(1.5) - 1 5 0.50 1.6 with 20 nodes. What is the maximum of the computed y vector on this domain, accurate to 3 decimal places (do But Hinil: First plot your solution to see if the boundaries look right. Hint 2: Ascume an ODE of the form dy By +ey - f(z) The transformation matrices are: M2 - (ding( -2 . mes(N, 1), 0) + diagloves(N - 1, 1), -1) + ding(ones (N - 1, 1). 1))/da MI = (ding(ones(N - 1, 1), 1) - ding(ones(NV - 1,1). -1))/(2 . dx); MO = eye(N); M = 0M2+61 + CMO;Questions are to be solved using MATLAB The code provided solves the boundary value problem d.x2 = x' cos(x), y(1) = 1, y(5) = 2 . on the interval 7